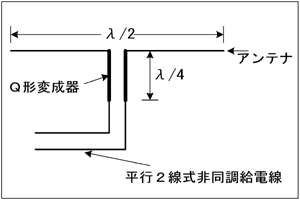
| □ H11年04月期 A-22 Code:[HH0201] : Qマッチセクション(Q形変成器)の動作原理とインピーダンス計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
|
Qマッチセクションの問題ですが、ほとんど出題されていません。ですが、原理的には単純で構造もシンプルに整合が取ることができます。マジメにやろうとすれば伝送線路方程式から話を始めなければなりませんが、ここでは任意の長さの伝送線路の先に、あるインピーダンスの負荷が繋がっている時の、電源から見たインピーダンスは、公式として与えられているものとして考えます。 ちなみにQマッチのQは、1/4を表す英語のquaterで、λ/4の伝送線を使うところから来ています。 [1]インピーダンスマッチングの本質とは?我々が運用する時は、送信機が「電源」で、アンテナが「負荷」で、その間を伝送線路(=ケーブル)で繋ぎます。定電圧電源を負荷に繋ぐ場合と違い、高周波回路では「インピーダンスマッチング」を取らなければならない、というのはご存知かと思います。送信機、ケーブル、アンテナにはそれぞれ送信周波数におけるインピーダンスがあり、これが整合していないと、送信機から出たエネルギーが100%アンテナから放射されません。 この問題で取り上げているのは、ある特性インピーダンスを持った、λ/4の長さの伝送線路を用いることで、送信機とアンテナを整合させることができる、という技術です。 [2]インピーダンスZ0 [Ω]のケーブルにR [Ω]の負荷を繋いだら…では、この問題を解く前に、特性インピーダンスがZ0 [Ω]で、長さがλ/4 [m]の伝送線路の先に、R [Ω]の負荷が繋がっている場合、「送信機から見て」何Ωに見えるのか?を考えてみましょう。 | |
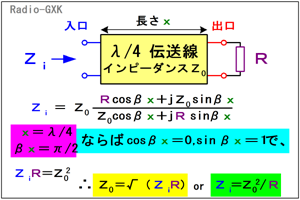 Fig.HH0201_a 送信機から見た伝送線路と負荷 |
送信機から負荷を見たインピーダンスと、送信機の出力インピーダンスが等しければ「整合が取れている」ということになります。 「ミソ」は、「送信機から見て」というところです。送信機に繋がっているのはZ0の特性インピーダンスのケーブルで、必ずしも送信機の出力インピーダンスとは同じにならないのですが、λ/4先にある負荷Rを含めて考えると、送信機にはあたかも自分と同じインピーダンスの負荷が接続されて見えるように、Z0やRを組合せで選ぶことができる、というわけです。 |
|
一般に、伝送線路の長さをx [m]として、送信機から見たこの系のインピーダンスをZiとすると、 Zi=Z0(Rcosβx+jZ0sinβx)/(Z0cosβx+jRsinβx) …(1) となります。(この式は、「伝送線路方程式」というものを解いて得られますが、その導出は1アマレベルでは不要ですのでここではやりません。) [3]長さが四分の一波長なら事情は簡単にβは定数で、β=2π/λです。(1)は虚数が出てきて面倒そうな式ですが、x=λ/4だとすると、途端に簡単になります。というのは、x=λ/4なら、βx=π/2となり、sinやcosが1や0という簡単な数になるからです。つまり、cosのかかっている項はゼロなので消えてしまい、sinの項のみが残ります。さらに、分母と分子にはjのかかった項だけになるので、jは消えてしまいます。では、(1)式にβx=π/2を代入して簡単にすると、 Zi=Z0(Z0/R) =Z02/R …(2) 普通、送信機やアンテナのインピーダンスは決まっていて、「Qマッチセクションのインピーダンスをいくらにするか」という手順で設計します。そこで、(2)をZ0について解けば、 Z0=√(ZiR) …(3) つまり、Z0は送信機の出力インピーダンスとアンテナのインピーダンスの相乗平均にすれば整合が取れる、ということになります。 例によって、このページでは「何故そうなるか」を追求したいので、虚数の出てくる(1)のような式をいじくり回して(3)式を導きましたが、試験に合格するだけなら(3)だけを暗記しておけばよいでしょう。 さて、ここで余談です。 送信機から見たインピーダンスZiは計算できたのですが、アンテナ側から見たらどうでしょうか? この場合も全く同様にして、電源側にZiというインピーダンスが繋がっている場合の、負荷から見たインピーダンス、すなわち(2)式をRについて解けばよいのです。 この系が「整合が取れている(マッチングしている)」ということは、送信機側から見ると送信機の出力インピーダンスと同じインピーダンスが、アンテナ側から見るとアンテナと同じインピーダンスが、それぞれ繋がって見える、ということなのです。 また、波長は速度係数をかけたものでなければならないことに注意します。つまり、波長は真空中の波長ではなく、ケーブル上の波長です。 それでは、解答に移ります。 この問題では、上の解説でいうZ0が求めるQマッチセクションに使う伝送路のインピーダンスZで、上の解説のZiは問題文の平行2線の給電線のインピーダンスZ0です。(3)式をこれに沿って書き直せば、 Z=√(RZ0) となりますから、正解は3と分かります。 | |
 |
 |