スーパーヘテロダイン受信機近接周波数選択度の向上中間周波増幅器の段数同調回路のQ シェープファクタ中間周波トランス(IFT) - １アマの無線工学 H12年08月期 A-15

□ H12年08月期 A-15 Code:[HF0601] : スーパーヘテロダイン受信機の近接周波数選択度の向上方法

検索サイトから来た方は…
無線工学の基礎トップへ

以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます

■ 無線工学を学ぶ

(1) 無線工学の基礎

年度別出題一覧

H11年 4月期,8月期,12月期

H12年 4月期,8月期,12月期

H13年 4月期,8月期,12月期

H14年 4月期,8月期,12月期

H15年 4月期,8月期,12月期

H16年 4月期,8月期,12月期

H17年 4月期,8月期,12月期

H18年 4月期,8月期,12月期

H19年 4月期,8月期,12月期

H20年 4月期,8月期,12月期

H21年 4月期,8月期,12月期

H22年 4月期,8月期,12月期

H23年 4月期,8月期,12月期

H24年 4月期,8月期,12月期

H25年 4月期,8月期,12月期

H26年 4月期,8月期,12月期

H27年 4月期,8月期,12月期

H28年 4月期,8月期,12月期

H29年 4月期,8月期,12月期

H30年 4月期,8月期,12月期

R01年 4月期,8月期,12月期

R02年 4月期,9月期,12月期

R03年 4月期,9月期,12月期

R04年 4月期,8月期,12月期

分野別出題一覧

A 電気物理, B 電気回路

C 能動素子, D 電子回路

E 送信機, F 受信機

G 電源, H アンテナ&給電線

I 電波伝搬, J 計測

■ サイトポリシー

■ サイトマップ[1ama]

■ リンクと資料

■ メールは下記まで

2022年

12/31 12月期問題頁掲載

09/01 08月期問題頁掲載

05/14 04月期問題頁掲載

H1208A15 Counter

無線工学 > １アマ > H12年08月期 > A-15
A-15	次の記述は、スーパヘテロダイン受信機の近接周波数選択度を向上させる方法について述べたものである。このうち誤っているものを下の番号から選べ。

１	中間周波数はできるだけ低い周波数とする。
２	中間周波変成器の同調回路のＱを小さくする。
３	中間周波増幅器の段数を増やす。
４	中間周波増幅器にクリスタルフィルタ又はメカニカルフィルタを使用する。

スーパーヘテロダイン方式の選択度に関する問題は、この近接周波数によるもののほか、影像周波数のよるものもからめて出題されることが多いものです。この問題を理解するには、交流回路のうち、共振回路のＱについてよく理解しておきましょう。\100万のHF機も\100ショップのAMラジオも、「要らない信号を排除する」回路は共振回路の組合せでできています。［１］近接周波数混信と影像周波数混信ここで問われているのは、「近接」の方ですが、まずは「近接」と「影像」について、どちらがどんなものか、簡単に復習しておきます。近接周波数混信受信したい信号（希望波）と妨害波が近い周波数にあるために起こる混信影像周波数混信希望波と中間周波数の差と、妨害波と中間周波数の差がほとんど同じになるために起こる混信。希望波と妨害波とは周波数的には近くない　これらは、全く性質の異なる混信で、後にも書きますが、対策がトレードオフになる部分もあります。性質の違いをよく理解しておくことが必要です。ちなみに、影像周波数混信はヘテロダイン方式の受信機にのみ特有の混信です。　近接周波数混信に関する問題は、「近い周波数にある混信をいかに取り除くか」を考えればよいわけです。［２］中間周波数の高低と選択度の関係　まず、中間周波数の高低と選択度について考えてみます。　今、21.300 [MHz]に受信したい信号があり、21.305 [MHz]に妨害波があるとします。わずか5 [kHz]しか離れていませんから、いわゆる「サイドがバサッと切れるフィルタ」でないとバリバリいって取れません。後にも述べる「スカート特性」（シェープファクタとも言い、帯域外の信号をどれだけ減衰させられるかの指標）のよい帯域外減衰特性が必要になります。　中間周波数が8.83 [MHz]だとすると、中間周波増幅段で分別すべき周波数は、8.830 [MHz]（信号波）と8.835 [MHz]（妨害波）となります。つまり、8.83 [MHz]に対しての5 [kHz]の差ですから、わずか0.06%の差をフィルタリングしなくてはなりません。　一方、中間周波数を455 [kHz]とするとどうでしょうか。今度は455 [kHz]（信号波）と460 [kHz]（妨害波）となります。つまり、455 [kHz]に対しての5 [kHz]の差ですから約1.1%で、この程度ならLCで構成した共振回路でも何とかフィルタリングできそうです。このことは、もっと定量的には以下のように説明されます。
フィルタ回路を構成するのは、共振回路です。LCだけではなく、クリスタルや表面弾性波フィルタでも等価回路は共振回路です。共振回路のＱは中心周波数をｆ₀、中心周波数の信号電圧の1/√2となる周波数をそれぞれｆ₁，ｆ₂（但し、ｆ₁＜ｆ₂）とすると、次式で表されます。　Ｑ＝ｆ₀/(ｆ₂－ｆ₁)　…(1) これを変形すると、　ｆ₂－ｆ₁＝ｆ₀/Ｑ　…(2) となります。	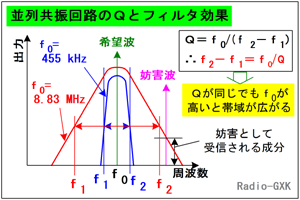Fig.HF0601_a 共振回路が持つ周波数選択効果とＱ
この式の意味するところは、Ｑが同じで中間周波数（＝中心周波数ｆ₀）が異なる２つのフィルタがあるとすると、通過帯域ｆ₂－ｆ₁の幅は、ｆ₀に比例するというものです。普通、通過帯域の幅はSSBかCWかなど、信号の種類によって決まり、中間周波数に左右されるものではありません。この観点（通過帯域幅＝ｆ₂－ｆ₁＝一定）からみれば、(2)式の意味は「中間周波数を高く取りたければ、それにつれてＱも大きくせよ」ということになります。　先の例で簡単に計算すると、-3dB帯域幅が3 [kHz]のフィルタを実現するのに、中心周波数が8.83 [MHz]なら、Ｑは約2940も必要ですが、455 [kHz]なら約152で済みます。　このことから、小さなＱでも通過帯域を狭く取れる、低い中間周波数が有利であることがわかります。　いろいろなリグやオプションのフィルタ類をご検討されたことのある方ならお分かりかと思いますが、フィルタの特性のうち、-6 [dB]の通過帯域幅f₆と-60 [dB]の通過帯域幅f₆₀の比f₆₀/f₆をシェープファクタといい、１よりも大きい値になりますが、１に近いほど-60 [dB]での帯域幅が-6 [dB]での幅に近いことを意味しますから、帯域外での減衰傾度（いわゆるスカート特性）が良好であることを意味します。　この問題とは別に、影像周波数混信に対しては、中間周波数は高い周波数の方が有利です。これに関する選択肢も出てきますから、どちらがどうだったか、頭の中でこんがらがってしまわないよう、原理から理解した方がいいでしょう。［３］中間周波トランスのＱと帯域の関係　次に、中間周波トランス（中間周波変成器。以下、IFTと書きます）のＱについて考えてみます。
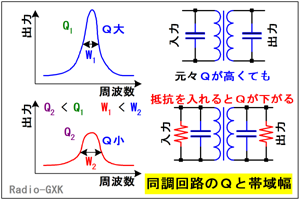Fig.HF0601_b 同調回路（IFT）のＱと帯域幅	IFTはFig.HF0601_b上のような構成になっているのが普通です。実際は共振周波数調整のため、コアの出し入れができたり、コンデンサがトリマになっていたりしますが。　この回路の共振特性はIFTの左にあるグラフのようになっています。この図から、選択度を高めるには、この山の形を鋭くすること、すなわち回路のＱを大きくすればよいことがわかります。　ところが、共振回路に並列に抵抗を入れると、Ｑが下がってしまいます（Fig.HF0601_b下）から、通過帯域が広がってしまいます。
普通こんな設計はしません。また、クリスタルフィルタやメカニカルフィルタは、水晶や金属片の電気機械現象の共振を利用していますが、この共振のＱは非常に大きく、選択度の高い（シャープな）フィルタを構成することができます。　関連した余談ですが、中間周波トランスは、結合度の調整でも伝送する帯域を変化させられます。定性的に言うと、結合を密にすると帯域が広くなり、逆に、結合を疎にすると帯域が狭くなります。このような選択肢もあるので、注意して下さい。［４］中間周波増幅の段数と帯域幅の関係
最後に、中間周波増幅器の段数について考えてみます。　中間周波数増幅器の段間は、一般に増幅器の間をフィルタやIFTで結合します。これらは、上にも書いたように周波数選択性を持っていますから、複数接続すると帯域内の信号のみが残って、帯域外の成分はどんどん減衰して行きます。これは、周波数特性がフィルタやIFTの特性の乗算となるからです。　もちろん回路が複雑化＝コストアップしますし、IFTなどには減衰もありますから、よいことばかりではありませんが、近接混信を避ける解としては正解です。	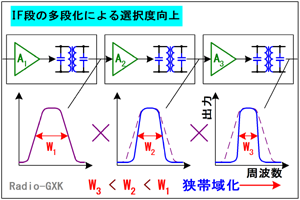Fig.HF0601_c 同調回路（IFT）の多段化と帯域幅
何段も重ねれば、スカート特性（国家試験では「減衰傾度」という用語が使われます）が良くなるのはクリスタルフィルタでもLCフィルタでも同じです。実際、高価なフィルタは多段で構成されています。それでは、解答に移ります。　１…IFは低い方が近接周波数には有利ですので正しい記述です　２…同調回路のＱを小さくすれば帯域が広まるので、誤りです　３…IF増幅段を増やせば帯域外特性が改善されますから、正しい記述です　４…これらのフィルタはスカート特性が良いので、正しい記述ですとなりますから、正解（誤った記述）は２と分かります。