| □ H12年12月期 A-01 Code:[HA0307] : 3個以上のコンデンサの合成容量・最大耐電圧・未知の静電容量等の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
|
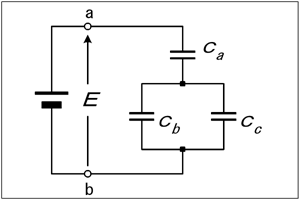
合成容量を求めろ、というなら簡単ですが、各コンデンサの端子電圧から容量の関係を求めるとなると、ちょっと面倒ですね。でも、一つ一つ潰して行けば、さほど難しくない問題であることが分かります。 (問題ではコンデンサCa, Cb, Ccの容量がそれぞれ、C1, C2, C3だといっていますが、この解説では、C1〜C3と書けば、コンデンサの名称と容量の両方を指すものとします。) [1]複数あるものはまとめてシンプルにする | |
|
コンデンサが3つもあると面倒なので、比較的簡単に合成できるC2とC3をまとめてFig.HA0307_bのように一つのコンデンサC23としてしまいます。並列接続ですから、容量は加算する(C23=C2+C3)だけです。こうすることで、直列の2つのコンデンサの問題に置き換わりました。 次に、これら2つコンデンサの両端にかかる電圧を考えます。そのためには、直列に接続されるコンデンサでは、各々のコンデンサに蓄えられる電荷がどうなっているか、を考えます。 |
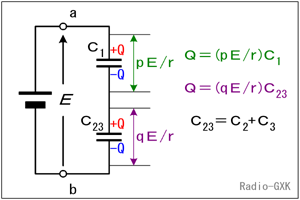 Fig.HA0307_b 容量を合成し単純化 |
[2]直列接続のコンデンサの各電極に蓄えられる電荷は等しいこの「証明」は簡単で、例えば、Fig.HA0307_bで、C1の電源側の電極に+Qの電荷が溜まったとすると、その対向する電極には−Qが溜まります。またC23の図の上側の電極には、+Qが溜まります。このノードは他にどこにも繋がっていないので、電子が勝手に消えたり湧いて出たりしない限り、一方に+Qがあれば他方には−Qがあって、合計がゼロになるはずだからです。また、C23の電源側の電極には−Qが溜まります。問題により、C1とC23それぞれの両端にかかる電圧が与えられていて、(上記から)そこに溜まる電荷量も分かっていることになるので、容量が計算できるはず、という算段になります。 それでは、解答に移ります。 問題が、C1の両端の電圧がE/5だと言っているので、C1に溜まる電荷量Qは、 Q=(E/5)C1 …(a) です。C2とC3(C23)には、残りの電圧(4E/5)がかかっているはずですから、 Q=(4E/5)C23 …(b) ここで、Fig.HA0307_bでp=1,q=4,r=5です。(a)=(b)と置いてQを消去すれば、 (E/5)C1=(4E/5)C23 …(c) また、 C23=C2+C3…(d) ですから、(d)を(c)に代入すれば、 (E/5)C1=(4E/5)(C2+C3) …(e) となります。(e)を整理して、 C1=4C2+4C3 となるので、正解は4と分かります。 なお、この問題では、容量の絶対値は分かりません。C1=8 [μF], C2=C3=1 [μF]でも成り立ちますし、C1=16 [pF], C2=C3=2 [pF]でも成り立ちます。C1, C2, C3はそれぞれ比率しか分からないのです。 | |
 |
 |