| □ H12年12月期 A-14 Code:[HE0302] : AM変調で、無変調時の出力電圧と変調度から、変調時の出力電圧を求める公式 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
| |||||||||||
AM(DSB)変調の変調度(率)と電力、又は、変調波の振幅の問題はよく出されます。SSBはAMに比べて電力効率が4倍も良いと言われていますが、それがなぜなのか、確認してから問題にかかりましょう。[1]AM変調における搬送波と側波帯の振幅成分単一正弦波で変調した時、電力を基準に考えると、搬送波が(電力比で)1だとすると、変調度が1(100%)でも両側波帯の占める電力は0.5(1/2)、単側波帯では0.25(1/4)にしかなりません。このことを、計算で確かめてみましょう。 まず、搬送波の電圧(最大値)をVc、角周波数をωc、信号波の電圧(最大値)をVs、角周波数をωs、変調度をmとします。この時、搬送波の瞬時値vcと信号波の瞬時値vsはそれぞれ、 vc=Vcsinωct …(1) vs=Vscosωst …(2) また、振幅については、定義から Vs=mVc ∴ m=Vs/Vc …(3) と表せます。変調波の瞬時値をvamとすると、 vam=(Vc+vs)sinωct =Vc{1+(Vs/Vc)cosωst}sinωct =Vc(1+mcosωst)sinωct …(4) さらに、(4)式を三角関数の和の公式を使って展開して、 vam=Vcsinωct+mVccosωstsinωct =Vcsinωct+(mVc/2){sin(ωc+ωs)t+sin(ωc−ωs)t} =Vcsinωct+ (mVc/2)sin(ωc+ωs)t+(mVc/2)sin(ωc−ωs)t …(5) (5)式において、赤字が搬送波、青字が上側波帯、緑が下側波帯の成分ということになります。 [2]搬送波の電力、側波帯の電力これらは、電圧比ですから、電力比に直してみましょう。 | |
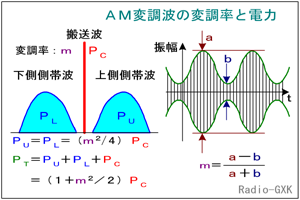 Fig.HE0302_a AM変調波の変調率と電力 |
本当は時間で積分しなければなりませんが、これらのどの成分も同じインピーダンスZの負荷(例えばアンテナ)に流れ込むので、比を求めるなら単に電圧の2乗比でよく、 搬送波電力 Pc=Vc2/2Z …(6) 上側波帯電力 PU=(mVc/2)2/2Z …(7) 下側波帯電力 PL=(mVc/2)2/2Z …(8) となります。 |
|
当然のことながら、上側波帯と下側波帯は対称なので、(7)と(8)からも分かりますが、それらの電力は等しく、 PU=PL …(9) です。また、Pcに対するPUやPLの比率は、 PU/Pc=PL/Pc ={(mVc/2)2/2Z}/(Vc2/2Z) =m2/4 …(10) となりますから、確かに、変調率m=1の時、単一の側波帯の電力は搬送波の1/4になっていることが分かります。しかも、mの二乗なので、m=0.7では約1/8になってしまいます。全電力PTを搬送波電力Pcで表せば、 PT=Pc+PU+PL=Pc(1+m2/2) …(11) となります。これで、変調度と搬送波電力が与えられた時のAM波の電力、あるいは、搬送波電力とAM波の電力が分かっている時の変調度の計算などが可能になりました。 それでは、解答に移ります。 この問題は、実効値の2乗が電力に比例することに気づくことがキーポイントです。 変調度をM、変調をかけた時の実効値をEm、搬送波のみの実効値をEcとすると、次が成り立ちます。 Ec2:Em2=1:(1+M2/2) ∴ Em=Ec√(1+M2/2) となるので、5が正解と分かります。 | |
 |
 |