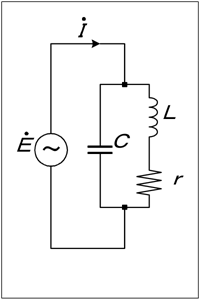
| □ H13年12月期 A-05 Code:[HB0401] : 損失のある並列共振回路。励振電流と電源電圧の関係、共振時の数値計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||
この問題で問われているのは、コイルに損失がある場合の共振回路についてです。その前に、まずコイルに損失のない回路モデルで「共振とは何か」を考えた後、問題の回路にかかりましょう。第1部 共振回路を学ぶ前に[1]『共振』を学べば高周波回路が分かる高周波回路、ことに無線に関係する回路の動作や無線機・アンテナの調整にいたるまで、この「共振」という現象と「回路のQ」という言葉抜きにしては語れません。長くなりますが、「そもそも回路が共振するというのはどういうことか」ということから始めます。これを理解していれば、フィルタ回路や、送受信機の回路動作など、他のジャンルの問題を解くことが可能になります。[2]基本的事項の確認…直列と並列共振回路と表記まず基本的な事柄の確認です。回路の共振には、Fig.HB0401_a左のような直列共振と、その右のような並列共振があります。無線の回路で多く見られるのは並列共振回路の方です。 | |
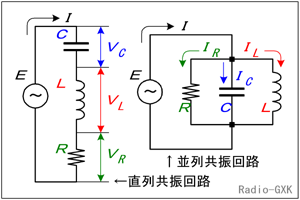 Fig.HB0401_a 直列・並列共振回路 |
この後必要になるポイントですから、ここでよくこの両者を見比べてみて欲しいのですが、「直列」の方はLCR三素子に共通なのは流れている電流です。途中で電子が増えたり減ったりはしませんから、これは明らかです。一方、並列の方では三素子にかかる電圧が共通です。これも、3つとも同じ電源に繋がれているので当然といえば当然です。 以下の図では、交流回路ですから、電流・電圧をベクトルで表記します。この方法に慣れていない方は、是非ともベクトル表記に慣れて下さい。 |
|
私も高校生時代に「交流理論」なる本を借りて読んだ時は、ワケが分からず瞬間睡眠したものですが、今になってこんな便利なものがあるのか、と思います。 余談はさておき、「直列共振回路では、各素子に流れている電流は同じだが、素子の両端に生じている電圧は各々大きさも向き(ここで言う「向き」は電圧ベクトルの向きなので、実は位相のこと)も違う」「並列共振回路では、各素子にかかる電圧は同じだが、素子に流れる電流は各々大きさも向きも違う」ということを頭に入れて下さい。 電源電圧や電流、各素子にかかる電圧や流れる電流をFig.HB0401_aのように取ります。図の中の斜体文字の電圧や電流はベクトル量であることを示します。文章の中では基本的にはすべてベクトル量(複素数)とします。 第2部 直列共振回路について[1]回路のインピーダンスと共振周波数Fig.HB0401_a左の直列共振回路の合成インピーダンスZsを考えます。直列ですから単純にRCL各素子のリアクタンスをXR=R,XC=−1/(ωC),XL=ωLとして足せばよいので、Zs=XR+j(XC+XL) =R+j(ωL−1/ωC) …(1) となります。共振周波数を求めるには、Zsの大きさが最小になればよく、虚数部分(青字の部分)=0と置いて、共振周波数fRを求めれば、よく知られた fR=1/{2π√(LC)} …(2) が出ます。ところで、さらりと「虚数部分をゼロにすればいい」と書いてしまいましたが、これは非常に深い意味を持ちます。この後も何度か出てきますから、意味を理解して下さい。 「インピーダンスの虚数部分をゼロにする」ということの意味は、電源にそのインピーダンスを負荷として接続した時、電圧の位相と電流の位相がずれないようにできる、ということを意味します。相手が抵抗だけであれば位相はずれませんが、インダクタンス分やキャパシタンス分が含まれると、電圧に対して電流が遅れたり進んだりします。つまり、「共振させる」ということは、インダクタンス分とキャパシタンス分が逆符号で打ち消しあうような回路の状態にする、ということを意味します。 一方、電源電圧Eは、(共振していようがいまいが)全ての素子の両端に生じた電圧の(ベクトル的な)和ですから、 VR=IR VC=−jI/ωC VL=jωIL と置いて、 E=IZs=I{R−j/(ωC)+jωL} =VR+VC+VL …(3) と表せます。共振した時は、(3)式の中にjの項(青字の項)がゼロになってしまう、ということです。 [2]電源周波数と回路の動作下のFig.HB0401_bを見ながら考えて行きましょう。 | |
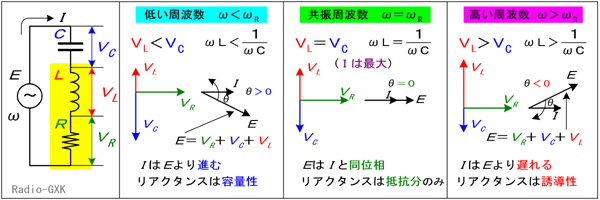 Fig.HB0401_b 直列共振回路と電源周波数 | |
(1) 電源周波数が共振周波数より低い時まず、電源周波数ω(=2πf)が共振周波数ωR(=2πfR)より低い時は、容量性リアクタンスXC(=1/ωC)と誘導性リアクタンスXL(=ωL)を比べると、XC>XLとなっています。要するに、周波数が低いので、コンデンサのリアクタンスよりコイルのリアクタンスの方が小さいのです。ここで、前の方で挙げた、「直列回路では流れる電流が全素子に共通」ということを思い出して下さい。電流Iが共通ですから、リアクタンスの大きい方、すなわちコンデンサの両端の電圧の方がコイルのそれより大きくなります。この状態をベクトル図で描くと、Fig.HB0401_b左のようになります。VLとVCは、向きが互いに逆で、その大きさを比べると、VL<VCです。電源電圧ベクトルEは、(3)式で表されますから、この図で行くと水平線(抵抗両端電圧VRや電流Iの向き)より下に来ます。つまり、電源電圧Eを基準にすると電流Iは(位相が)進んでいるという状態になります。(ちなみに、抵抗の両端の電圧VRと電流Iの位相は同じです。)このような状態を、回路のリアクタンスは容量性であるといいます。式で言うと、(1)式のjの係数が負、ということになり、電源から見ると、キャパシタンス分が多く見える、ということです。 (2) 電源周波数が共振周波数より高い時上とは全く逆の理由で、XC<XLとなります。今度は、周波数が高いので、コイルのリアクタンスよりコンデンサのリアクタンスの方が小さいのです。また、コイルの両端の電圧の方がコンデンサのそれより大きくなります。この状態をベクトル図で描くと、Fig.HB0401_b右のようになります。VL>VCです。電源電圧ベクトルEは、水平線より上に来ます。つまり、電源電圧Eを基準にすると電流Iは遅れているという状態になります。このような状態を、回路のリアクタンスは誘導性であるといいます。式で言うと、(1)式のjの係数が正、ということになり、電源から見ると、インダクタンス分が多く見える、ということです。(3) 電源周波数が共振周波数と等しい時この状態が「共振状態」です。容量性リアクタンスと誘導性リアクタンスは、XC=XLの状態で、コンデンサの両端の電圧とコイルのそれが大きさが等しくなります。この状態をベクトル図で描くと、Fig.HB0401_b中のようになります。VLとVCは、向きが互いに逆で、大きさが等しいので、ベクトルの和では零となり、合成後のベクトル中には図の垂直方向の成分は現れてきません。すなわち、回路は誘導性でも容量性でもなくなり、式で言うと、(1)式のjの係数が0、ということになって、電源から見ると、抵抗しか繋がっていないように見える、ということです。 この時、回路で起こっている物理的な現象は何か、というと、コンデンサやコイルはそれぞれ電界(電気力線)や磁場(磁力線)、という形でエネルギーを蓄える装置ですが、これらは互いに振動する逆方向の電圧(電流は共通)に応じてエネルギーをやり取りしています。「電圧が最大の時に最大のエネルギーを蓄えるコンデンサ」と、「電流が最大の時に最大のエネルギーを蓄えるコイル」が、互いに180°ずれた電圧を振動させながらエネルギーをやり取りしているわけです。この振動数は容量とインダクタンスで決まります。共振状態では、この2個の素子の持つ固有の振動数と電源周波数がぴったり合うため、外(電源)から見ると同じ大きさで逆向きの電圧が合成された結果、見えなく(0 [V])なり、抵抗分だけが残るというわけです。 従って、回路全体のインピーダンスは最小になりますから、電流Iの大きさは最大となります。(このあたりのことは、この後の「回路のQ」でご説明します。) 第3部 並列共振回路について[1]回路のインピーダンスと共振周波数これもFig.HB0401_a右の回路を元に合成インピーダンスZpから考えて行きます。並列ですからアドミッタンス(インピーダンスの逆数)で考えた方が分かりやすいですね。合成アドミッタンスYpは、RCL各素子のリアクタンスをXR=R,XC=−1/(ωC),XL=ωLとして、 Yp=1/Zp =(jXRXL+XLXC+jXCXR)/(XRXLXC) =1/R+j{ωC−1/(ωL)} …(4) ∴ Zp=[1/R+j{1/(ωL)−ωC}]/[(1/R)2+{ωC−1/(ωL)}2] …(5) 共振周波数を求めるには、Ypの大きさが最小になればよく、(5)式の虚数部分(青字の部分)=0と置く方法は直列共振の時と同じ手法です。その結果、共振周波数fRを求めれば、直列共振の時と全く同じ方程式になり、 fR=1/{2π√(LC)} …(2) が出ます。また、電源電流Iは、共振しているか否かに関わらず、全ての素子に流れる電流の(ベクトル的な)和ですから、 IR=E/R IC=jωCE IL=E/jωL と置いて、 I=E/Zs=EYp=E[1/R+j{ωC−1/(ωL)}] …(6) =IR+IC+IL …(7) と表せます。ここでも、着目すべきは、共振時は虚数部分(青字の部分)がゼロになることです。ここまで見てくると、直列共振も並列共振も、本質は変わらない、ということにお気づきかと思います。 [2]電源周波数と回路の動作下のFig.HB0401_cを見ながら考えて行きましょう。 | |
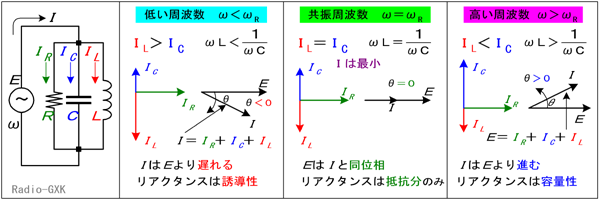 Fig.HB0401_c 並列共振回路と電源周波数 | |
(1) 電源周波数が共振周波数より低い時まず、電源周波数ω(=2πf)が共振周波数ωR(=2πfR)より低い時は、容量性リアクタンスXCと誘導性リアクタンスXLを比べると、XC>XLとなっています。周波数が低いので、コンデンサのリアクタンスよりコイルのリアクタンスの方が小さいのです。ここまでは直列共振の時と全く同じです。ここで、前の方で挙げた、「並列回路では全素子にかかる電圧が共通」ということを思い出して下さい。電圧Eが共通ですから、リアクタンスが小さい方、すなわちコイルに流れる電流の方がコンデンサのそれより大きくなります。この状態をベクトル図で描くと、Fig.HB0401_c左のようになります。ILとICは、向きが互いに逆で、その大きさを比べると、IL>ICです。電源電流ベクトルIは、(7)式で表されますから、この図で行くと水平線(抵抗の電流IRや電源電圧Eの向き)より下に来ます。つまり、電源電圧Eを基準にすると電流Iは(位相が)遅れているという状態になります。ですから、回路のリアクタンスは誘導性となっています。式で言うと、(5)式の分子のjの係数が正、ということになり、電源から見ると、インダクタンス分が多く見える、ということです。 (2) 電源周波数が共振周波数より高い時上とは全く逆の理由で、XC<XLとなります。今度は、周波数が高いので、コイルのリアクタンスよりコンデンサのリアクタンスの方が小さいのです。また、コンデンサに流れる電流の方がコイルのそれより大きくなります。この状態をベクトル図で描くと、Fig.HB0401_c右のようになります。IL<ICです。電源電流ベクトルIは、水平線より上に来ます。つまり、電源電圧Eを基準にすると電流Iは進んでいる状態になります。これは、回路のリアクタンスは容量性であるということになります。式でいうと、(5)式のjの係数が負、ということになり、電源から見ると、キャパシタンス分が多く見える、ということです。(3) 電源周波数が共振周波数と等しい時共振状態では、容量性リアクタンスと誘導性リアクタンスは、XC=XLの状態で、コンデンサに流れる電流とコイルのそれが大きさが等しくなります。この状態をベクトル図で描くと、Fig.HB0401_c中のようになります。ILとICは、向きが互いに逆で、大きさが等しいので、ベクトルの和では零となり、合成後のベクトル中には図の垂直方向の成分は現れてきません。すなわち、回路は誘導性でも容量性でもなくなり、式で言うと、(5)式のjの係数が0、ということになって、電源から見ると、抵抗しか繋がっていないように見える、ということです。 この時、回路で起こっている物理的な現象は何か、というと、コンデンサやコイルは互いに振動する逆方向(方向はFig.HB0401_a右のような方向を正とする向き)の電流に応じてエネルギーをやり取りしています。ちょうどシーソーのように、コンデンサとコイルの間を電流が行ったり来たりしているイメージです。この振動数は容量とインダクタンスで決まります。共振状態では、この2個の素子の持つ固有の振動数と電源周波数(位相も)がぴったり合うため、外(電源)から見ると、もし抵抗がなければ電流が全く入れず、あたかもコイルとコンデンサは両方とも無く(インピーダンス=∞)、抵抗しかないように見える、というわけです。 従って、回路全体のインピーダンスは最大(Rのみ)になりますから、電流Iの大きさは最小となります。(これもまた、この後の「回路のQ」でご説明します。) 第4部 共振回路と回路のQ共振回路といえば、必ずと言っていいほど問われるのが回路のQです。そもそも、Qって何?というところから始めたいと思います。私自身理解の不足なところでもありますが、端的に言ってしまえば「共振回路のL(コイル)分にどれだけ損失が少ないか」という指標です。この指標が大きいほど、共振回路としては理想的な動作に近づくわけです。ここで言う「損失」とは電流が熱になること、すなわち抵抗分です。先にコイルの損失、と書きましたが、実際にはC(コンデンサ)にも実装基板のパターンにも抵抗があるのですが、線が長く巻いてあるコイルが、最も抵抗分の多い素子なので、他は無視するケースが多いです。 ではまず、直列共振回路のQから。 | |
[1]直列共振回路の端子電圧とQ直列共振回路が共振している時は、Fig.HB0401_bの真中のベクトル図や等式不等式が成り立っています。式だけではよく分からないので、箇条書きで要約すれば、(1) コイルとコンデンサの両端の電圧は、大きさが同じで極性が逆 (2) 電源から見ると、抵抗しか繋がっていないように見える (3) 電流Iは電源電圧Eと同位相で、共振していない時に比べ最大値をとる ということです。ならば、コイルとコンデンサの両端の電圧と、抵抗の両端の電圧はどういう関係になっているのでしょうか? 抵抗の両端に生じる電圧の大きさはRI [V]、コイルの両端に生じる電圧の大きさは、IXL=ωLI [V]です。ちなみに、コンデンサの両端に生じる電圧の大きさもIXC=I/ωC [V]でコイルの電圧と同じです。ここで、両者(抵抗とコイル)の比率を取って、 Q=ωLI/RI=ωL/R …(8) という値を定義してしまいましょう。要するに、Qは抵抗の両端の何倍の電圧がコイル(またはコンデンサ)の両端に生じているかという値だというわけです。ちなみに、抵抗両端の電圧VRは電源電圧Eと位相も大きさも同じです。 実際のコイルとコンデンサのみ(抵抗がない)からなる直列共振回路では、Qが数10〜数100程度です。ということは、電源電圧が数[V]でも、コンデンサやコイルの両端には数100 [V]が発生する、ということですので、これだけの耐圧がないと絶縁破壊を起こします。バッテリー駆動のモービル機であっても、高周波出力回路の充電部に触れると危険だ、というのはこのあたりの原理に起因します。 [2]並列共振回路の素子電流とQこれまで、並列共振回路で、コイルには損失の無いものとして扱ってきましたが、ここからは損失のあるモデルで考えます。(1) コイルに損失のある並列共振回路のモデル直列共振の回路モデルと並列共振のモデルがありましたが、並列共振の回路モデルをFig.HB0401_d左のように変更します。 | |
|
普通、並列共振回路にFig.HB0401_aのように、わざわざ損失を招く並列抵抗を入れません。また、上で述べたように実際には、コイルに抵抗分がありますので、これを勘定に入れなければなりません。(この回路が、この問題で問われているものそのものになります。) 直列共振のモデルは、うまい具合にコイルと抵抗が直列に入っていて、これがそのまま抵抗を持つコイルを表しますので、モデルはそのままでよく、並列のモデルのみを変更します。 |
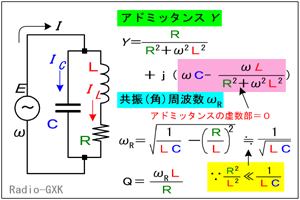 Fig.HB0401_d 損失のある共振回路 |
ただ、抵抗分がある、といってもインダクタンスと比較して無視できる程度であるのが通常(そんな抵抗分の多いコイルは使えない)なので、問題においては、R≪ωLという条件が付けられるのが普通です。この場合、モデルを変更する前の動作とほとんど同じです。この「ほとんど同じ」がどの程度同じなのかは、きちんと整理してみないと分かりません。そこで、ちょっと面倒になりますが、再び解析に挑戦します。(2) 損失を含んだ並列共振回路の解析並列回路ですので、アドミッタンスYで考えた方が楽です。コンデンサの枝(容量サセプタンス)=ωC、コイルと抵抗の枝=1/(R+jωL)ですから、ガチャガチャ計算すると、Y=jωC+1/(R+jωL) =R/(R2+ω2L2)+j[ωC−ωL/(R2+ω2L2)] …(9) 共振周波数ωRを求めるには、(9)式の虚数部分(赤字の部分)=0とおいて、ωについて解けば良く、これもガチャガチャ計算して、 ωR=√[1/LC−(R/L)2] …(10) このとき、青字の部分について見てみましょう。抵抗が無ければ、(R/L)2の項はゼロですから、共振周波数は2アマで出る式と同じになります。共振周波数が100 [kHz]とすると、ωR2はほぼ3.95×1011となります。L=10 [μH]とすると、概略C=0.25 [μF]となりますが、普通コイルの抵抗分は[mΩ]程度ですから、仮に大き目の100 [mΩ]として、(R/L)2=108となります。一方、1/LC=3.95×1011ですから、(R/L)2≪(1/LC)です。 つまり、通常の部品定数では、R=0 [Ω]とした時の共振周波数とほとんど変わらないわけです。 共振した時、アドミッタンスが最小、すなわち並列回路の合成インピーダンスが最大となり、実数部分((10)式の青字の部分)の逆数になります。つまり、共振時のインピーダンスZRは、 ZR=(R2+ωR2L2)/R …(11) (11)式のωRに(10)式を代入して、 ZR=L/CR …(12) という簡単な形になってしまいます。 (3) 解析結果の意味するところここでこの値をちょっと吟味してみると、まずこのインピーダンスには周波数が入っていません。ということは、共振時にはLCRの値だけで周波数に無関係にインピーダンスが決まる、ということです。通常我々の扱う周波数領域や実際に線を巻いたコイルでは、Rは[mΩ]から大きくても数 [Ω]です。一方、Lは[μH]から[mH]、Cは[pF]から[μF]ですからZRは103〜6 [Ω]という大きな値を取ることが分かります。では、今度は共振時にコイルに流れる電流ILと電源から流れ込む電流IRを比較してみます。回路のインピーダンスがZR [Ω]で電源電圧がE [V]ですから、IRは、 IR=E/ZR=ECR/L …(13) 一方、ILは、 IL=E/(R+jωRL) …(14) IRに対するILの比率を取ると、 IL/IR=L/{CR(R+jωRL)} =L(R−jωRL)/{CR(R2+ωR2L2)} …(15) ここで、はじめてR≪ωLという条件を使います。(逆にここまではこの条件無しで出してきました。)要するに、(15)式の青字の部分において、Rが無視できる、とするわけです。すると、(15)式(の絶対値)は非常に簡単(分母のωRに(10)式を代入するなどして)になって、 |IL/IR|=ωRL/R …(16) となります。 (4) コイルとコンデンサに流れる電流一段落して、コンデンサに流れる電流ICについても考えてみましょう。(9)式で、虚数部分=0と置きました。アドミッタンスの虚数部分がゼロ、ということは、インピーダンスの虚数部分もゼロです。インピーダンスの虚数部分がゼロならば、電源から流れ込む電流と電圧の位相差はゼロ、つまり同相です。ところが、コンデンサやコイルには虚数のインピーダンスを持ちますから、全体としてゼロだということは、コイルとコンデンサが互いに逆符号で同じ大きさの虚数分を持っていなければなりません。つまり、コイルとコンデンサの間に振動電流が流れ、この両者の両端に発生する電圧が、電源電圧と同相になっている、ということです。実はここの論理にはちょっとインチキがあります。最初に共振条件を(9)式の虚数部分がゼロとおいた時、すでに両者の電流が上に述べたような条件を満たすと決めてしまったようなものだからです。これが共振の本質なので、間違ってはいないのですが、ちょっと「臭いぞ」と思われた方のためにお断りしておきます。要するに、ICに対しても、 |IC/IR|=1/ωRCR(=ωRL/R) …(17) となります。 (5) 損失のある並列共振回路のQやっとここでQを定義します。直列共振回路で定義したのと同じように、Q=ωRL/R(=1/ωRCR) …(18) とすれば、共振時、コンデンサやコイルに流れる振動電流は、電源から流れる電流のQ倍となります。 並列共振回路が共振している場合について、直列の時と同様、動作を箇条書きで要約すれば、 (1) コイルとコンデンサに流れる電流は、大きさが同じで向きが逆 (2) 電源から見ると、L/CRの抵抗が繋がっているように見える (3) 電流Iは電源電圧Eと同位相で、ω≠ωRの時に比べ最小値をとる ということです。 [3]Qと共振特性(帯域幅)
共振回路というのはそのままで帯域フィルタです。Fig.HB0401_eの左半分が直列共振回路の共振特性です。共振周波数で電流が最大になり、それ以外はインピーダンスが上がり、電流が減ります。 | |
|
では、Qの大小で、この特性曲線はどう変わるのでしょうか? グラフの青い線がQが大きい時で、赤い線がQが小さい時です。Qが大きいほど山が高く、かつ細くなります。言い換えれば、帯域フィルタの帯域が狭くなり、スカートが立ちますから、シャープないわゆるシェープファクタが良いフィルタになります。 逆にQが小さいと、山が低くなり、すそが広がった特性になります。どの程度の帯域が欲しいかで、Qを制御してやれば、所望の特性が得られます。 |
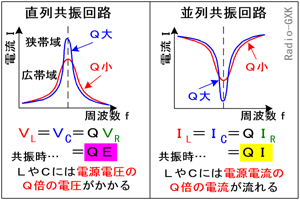 Fig.HB0401_e Qと周波数特性 |
|
並列共振回路においては、共振時の電流は最小値を取ります。この様子はFig.HB0401_e右のようであり、並列回路では直列共振と同じく、(9)式で定義したような抵抗分Rのあるコイル(インダクタンスL)のQに対して、共振曲線はやはりQが大きいほど共振曲線は鋭く、小さいほど広がりの大きな山の低いものとなります。 Qは共振曲線の山の頂上と比べて、1/√2となる高さの周波数(2つ)をf1,f2(f1<f2)とすると、次式を満たすことも知られています。 Q=fR/(f2−f1) …(18) ここではこの式の導出は行ないません(H2812A04で計算してみました)が、fRが決まっているなら、Qが大きい方が、通過帯域幅f2−f1が狭いことが分かります。 もう一つの注意点。よく、Qがカタログなどで表示されていることがあります。(8)式や(18)式を見てお分かりの通り、Qの定義にはωという周波数の項が入っていますので、周波数が規定されなければQが決まりません。ですので、用途が決まっているコイル(例えば10.7 [MHz]のIF用)では、大概の場合その周波数でのQですが、それ以外の場合はいくつの周波数でのQなのかについて、注意する必要があります。特に、フェライトなどのコアが入ったコイルでは、低周波までしか対応しないコアに高い周波数電流を流したりするとコアの中で損失が起こり、巻線抵抗は低いのにQが低くなる、といったトラブルも起こります。 ここまで読んでこられた方、お疲れ様でした。やっとこの問題の解答にたどり着きました。これまでの内容から、並列共振回路についての記述を読めば、 [A]は… 並列共振回路で、コンデンサに流れる電流(進み位相)がコイルに流れる電流(電源電圧より遅れ位相)より大きいのですから、全体として電源から流れ出る電流は、電圧に比べ進むのが正解です。 [B]は… 並列共振回路が共振している時、LCの間で「ピンポン」状にやり取りされている電流が電源と同位相の電圧を生じているため、電源からの電流は入りにくくなっています。ですから、電源電流は最小となります。 [C]は… CのリアクタンスがLのリアクタンスより大きいということは、電流で考えると、Cには電流がLより流れにくいのですから、[A]と逆の状況です。すなわち、電流が電圧より遅れているので、誘導性です。 となりますから、正解は1と分かります。 | |
 |
 |