| □ H13年12月期 A-17 Code:[HG0405] : ツェナーDiを用いた定電圧回路。最大電力、安定抵抗、最大電流等の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
安定化した電圧を作り出す、最もシンプルな回路はツェナーダイオードを使うことです。この問題にあるように、ツェナーダイオード一本と抵抗一本とで作れてしまいます。ただ、ここから大きな電力を取り出そうとすると、いろいろ厄介なことが出てきます。この問題では、そこを問うています。[1]ツェナーダイオードを用いた定電圧化の動作まず、その厄介な問題に入る前に、ツェナーダイオードを使った定電圧電源のことについて調べておきます。あまり難しいことはなく、オームの法則だけで解析できます。 | |
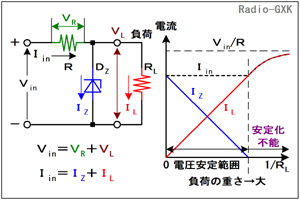 Fig.HG0405_a ツェナーを用いた定電圧動作の原理 |
まず、Fig.HG0405_aの左を見て下さい。電源電圧がVin、電源電流をIin、ツェナー電流をIZ、負荷電流をILとします。また、安定化抵抗Rの両端に発生する電圧をVR、負荷の両端に発生する電圧をVLとします。ツェナーダイオードのツェナー電圧はVZとします。 これらの関係を式にしてみると、Fig.HG0405_aの左下のような単純なものになります。すなわち、電圧で見れば電源電圧はVRと負荷にかかる電圧VLの和ですし、電流で見れば、電源電流はツェナー電流と負荷電流の和です。 |
|
この式は単純ですが、ツェナーダイオードを使っていることで、ある、「特殊な状況」が生じます。その「特殊な状況」とは、ツェナーダイオードの両端が、ツェナー電圧に保たれている条件では、電源電圧が変動しなければ、電圧の式、 Vin=VR+VL …(1) となります。また、抵抗Rに流れる電流Iinは、 Iin=VR/R …(2) となります。このIinは別の表現では、 Iin=IZ+IL …(3) と表され、これはツェナーダイオードと負荷に流れる電流の和は一定という意味です。 数式ばかりで話がややこしくなってきたので、グラフで整理してみます。Fig.HG0405_a右のグラフを見て下さい。横軸に1/RLを取っています。これはいわば「負荷の重さ」を示したもので、これがゼロならRLは開放(つまり無負荷)、無限大なら短絡を意味します。 今、無負荷から徐々に抵抗を小さくして行き、負荷を重くして行くことを考えます。 (1) 無負荷の時 無負荷の時は、電源から流れ込む電流は、全てツェナーダイオードを流れます。その電流の大きさIin0は、 Iin0=(Vin−VZ)/R …(4) となります。これだけの電流がツェナーダイオードを流れ、その両端にはVZの電圧が生じているので、ツェナーダイオードは、 P0=Iin0VZ …(5) なる電力P0を消費しています。 (2) 軽負荷の時 負荷を徐々に重くしてゆくと、ツェナーダイオードの電流IZは減少し、その分負荷電流ILが増加します。両者の和は一定(Iin0=VR/R)に保たれます。この範囲では、負荷にかかる電圧VLはツェナー電圧そのもので一定であり、この回路が定電圧電源として動作します。 ではどこまでの重さの負荷RL1に対してこの条件が成り立つかというと、 RL1=RVZ/(Vin−VZ) …(6) までです。RLがちょうどこの抵抗値の時に、ツェナーダイオードを流れる電流IZがゼロになります。これより重い負荷(=小さい抵抗R)ではこの回路はhfe電源として機能しなくなります(理由は以下に)。 (3) 重負荷の時 RLが 更に負荷を重く(RLが(6)より小さく)なり、流す電流を増やそうとすると、抵抗Rでの電圧降下が大きくなって、 Vin−VR<VZ …(7) となってしまい、既にツェナーダイオードの電流はゼロになっていますから、これはないのと同じです。つまり、電源にRとRLが直列に繋がっているだけの回路と同じなので、もはや負荷RLの変動に対して、その両端の電圧は定電圧ではなくなってしまいます。更に負荷を重くした極限として、短絡した時のことを考えてみましょう。電源電流はRでのみ制限されますから、 Iin=Vin/R …(8) となり、Fig.HG0405_a右のグラフでいうと、負荷をどんどん重くする極限(1/RL→∞)では、電流は(4)の値に漸近することになります。 上記では、負荷が変動するとして考えてみましたが、電源電圧が変動する場合は、以下のように考えます。 まず、ツェナー電圧が変動しないので、これに並列に繋がっている負荷の電圧も変動しないことから、定電圧性は保たれます。この時、(1)式を見ると、電源電圧が変動した分は、VRつまり安定化抵抗の両端の電圧の変動となって吸収されることが分かります。 一定値の抵抗Rの両端の電圧が変動するので、電源からの電流Iinは変動しますが、負荷の両端の電流ILは不変です。変動分はツェナー電流IZが変動することで吸収します。 [2]流し得る電流とツェナーダイオードの定格上で見たように、定電圧電源としてこの回路が動作するためには、制約条件があります。負荷が重過ぎると定電圧にならないからです。その条件は、(4)式でした。この時に負荷に流れる電流はいくらになるかというと、無負荷の時からRL=RL1になる時まで、電源から流れ出る電流はIin0で一定でしたから、負荷に流し得る最大電流は、(4)式で決まるIin0と等しい、ということになります。 ここで、なるべく大きな電力を負荷に与えたい、という観点で(4)式を見ると、入力電圧とツェナー電圧の差Vin−VZは大きい方が良く、また、安定化抵抗の値Rは小さい方が大きな電流が負荷に流せることが分かります。一方で、(5)式から、無負荷の時にツェナーダイオードでは最大P0の電力を消費するので、あまり大きなIin0とすると、小さなツェナーダイオードでは破損してしまいます。つまり、ツェナーダイオードの定格によって、流せる電流が制限されるのです。 今、ツェナーダイオードの最大電力定格をPmとして、流せる電流をImaxとすると、(5)式から、 Imax=Pm/VZ …(9) と求められます。これは、ツェナーダイオードに流せる最大電流であるとともに、負荷に流せる最大電流でもあります。上で見たように、これより多くの電流を流そうとして負荷抵抗値を下げれば、電圧が安定化されなくなってしまうからです。 ここまで見てきたように、ツェナーダイオードを用いた問題のような安定化電源は、負荷に電流が流れていない時も、ツェナーダイオードに電流が流れ、発熱していますから、効率が悪い電源です。また、ツェナー電圧は温度係数を持ちますので、温度に対する安定度もあまり良くありません。さらに、上で見たようにダイオードや抵抗の定格で決まる最大電力が存在して、大電力が取り出すのが容易でないため、小容量であまり精度の要求されない定電圧電源として用いられます。 この電源回路は、負荷の短絡に対して、ツェナーダイオードに流れる電流はゼロになるので、これに対する保護は不要ですが、安定化抵抗に電源電圧がモロにかかる(=Vin2/Rの熱が出る)ので、この耐電力を十分に取るか、ヒューズを入れるなどの保護が必要になります。 それでは、解答に移ります。 選択肢の組合せとして、抵抗値か電流値が決まればもう片方が決まるようになっていますから、どちらかが求められたら、もう一方で検算すればよいのです。 ここではまず簡単そうな最大電流ILmaxから求めてみましょう。なぜ電流の方が簡単かというと、ツェナー電圧VZと定格電力Pmが分かっていれば、(9)式から無負荷時の(ツェナーダイオードに流せる)最大電流Imaxが求められ、この値がそのまま負荷に流せる最大電流ILmaxでもあるからです。(9)式にVZ=12 [V]、Pm=1 [W]を代入して、 Imax=ILmax=1/12 [A]=83.3 [mA] となりますから、3が正しそうです。では逆に、Rが96 [Ω]だとして、83.3 [mA]が流れている時に、負荷の両端が12 [V]になるでしょうか? VL=Vin−VR=20−0.0833×96=12 [V] と確認できましたので、正解はやはり3と分かります。 | |
 |
 |