| □ H14年08月期 A-02 Code:[HA0205] : 点電荷の間に働く力の計算(クーロンの法則) |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
| |||||||||||
この問題で問われているのは、クーロンの法則そのものなので、数式を覚えていないと解けないでしょうが、覚えた数式を忘れないためにも、その意味を理解することをお勧めします。[1]クーロンの法則とその意味クーロンの法則は、式自体は割と簡単です。空間に2つの点電荷QA [C]とQB [C]があって、その間の距離がr [m]、QAとQB間が誘電率εの物質で満たされている時、クーロンの法則(磁気に関するクーロンの法則もあるので、正確には「静電気力に関するクーロンの法則」です)により、両者の間に働く力F [N]は、次式で表されます。F=QAQB/(4πεr2) …(1) | |
|
この式に、各々の変数を代入してしまえば答えは出るわけですが、その前に定性的な理解のため、この式をちょっと見てみます。 働く力の大きさFは、各々の電荷量の積に比例します。これは感覚的に理解できますね。また、Fの符号で吸引力か反発力かが分かります。2つの点電荷は異符号なら、F<0で吸引力が働きます。同符号ならF>0で反発力です。電荷の他に影響を及ぼす物体がなければ、働く力は作用と反作用の関係にありますから、各々の点電荷に働く力は、大きさが同じで向きが逆になります。 |
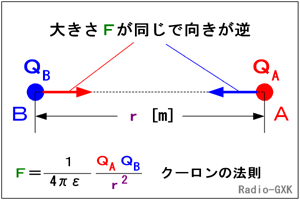 Fig.HA0205_a クーロンの法則 |
また、両者間の距離の2乗に反比例します。光っている電球など光源からの明るさと距離の関係と同じです。重力もアンテナから発せられる電波が作る電界強度もそうです。世の中には、相互の距離の2乗に反比例した影響力を持つ、という物理法則が非常に多いです。[2]物質固有の数…誘電率注目すべきは、もうひとつの分母である誘電率εです。問題が真空中なら真空の誘電率ε0を用いますが、空気や他の物質の中にある場合はその物質の誘電率εがここにきます。真空の誘電率より小さな誘電率を持つ物質はありません(すなわちε0<ε)から、真空の時と比べて周囲が物質に囲まれている状態では、εが大きな物質であるほど、力は弱くなります。それでは、解答に移ります QA=3 [μC]、QB=4 [μC]、r=0.2 [m]、ε0=(1/36π)×10-9をクーロンの法則(1)に代入すると、 F=(9×109)×(3×10-6)×(4×10-6)/0.22= 2.7 [N] となりますから、4が正解と分かります。 ここから先はまた余談ですが、この電荷量のクーロンという単位、この問題から見てもお分かりのように我々が扱う電気の世界では、ちょっとスケールがデカ過ぎます。なぜならば、この問題の答えの2.7 [N]という力は、地上で270 [g]程度のものの物体に働く重力に等しいわけです。 今回、この両者の電荷量が、3 [C]と-4[C]だとしたら、引き合う力は2.7×1012 [N]となって、地上での重さに換算すれば、約2,700万トンとなります。こんな巨大な力で引き合うものを、わずか20cmの距離には置いておけないですね。 | |
 |
 |