| □ H15年12月期 A-03 Code:[HA0307] : 3個以上のコンデンサの合成容量・最大耐電圧・未知の静電容量等の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
| |||||||||||
この問題では、「直列接続のコンデンサの各電極に蓄えられる電荷は等しい」、という物理が解法のキーになります。容量がすべて同じ場合以外は、耐圧100 [V]のコンデンサが3つ直列なんだから、300 [V]だろう、というのは間違いです。[1]直列接続のコンデンサの各電極に蓄えられる電荷は等しい各コンデンサの容量やかかる電圧をFig.HA0307_cのように置きます。 | |
|
直列接続のコンデンサの各電極に蓄えられる電荷は等しいので、Qと置きます。 なお、電荷が等しい理由の「証明」は簡単で、例えば、Fig.HA0307_cで、C1の電源側の電極に+Qの電荷が溜まったとすると、その対向する電極には−Qが溜まります。またC2の左側の電極には、+Qが溜まります。このノードは他にどこにも繋がっていないので、電子が勝手に消えたり湧いて出たりしない限り、一方に+Qがあれば他方には−Qがあって、合計がゼロになるはずだからです。C3についても同様です。 |
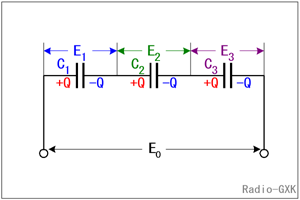 Fig.HA0307_c 直列コンデンサの電圧 |
[2]最小容量のコンデンサに最高電圧がかかるここで仮に、最も容量が小さいコンデンサがC1であるとして、これに最大電圧E1maxがかかっている時に、他のコンデンサにどれだけの電圧がかかっているかを計算します。まず、このときに各コンデンサに蓄えられる電荷Qを計算します。Q=E1maxC1 …(1) これと同じ電荷がC2, C3についても溜まりますから、これらの両端にかかる電圧をそれぞれ、E2, E3とすれば、 Q=E2C2 …(2) Q=E3C3 …(3) (1)と(2)、(1)と(3)からそれぞれQを消去すれば、 E1maxC1=E2C2 ∴ E2=(C1/C2)E1max …(4) E1maxC1=E3C3 ∴ E3=(C1/C3)E1max …(5) となります。 上記の結果を吟味してみます。C1が3つの中で最小容量のコンデンサなので、(4),(5)式の中で、C1/C2<1でかつ、C1/C3<1です。つまり、E2<E1maxでかつ、E3<E1maxということ、すなわち最も小さな容量のコンデンサに最大電圧がかかるので、複数の耐圧が同じコンデンサを直列につないで耐圧を稼ぎたい時、全体の耐電圧を決めているのは最小容量のコンデンサだ、ということです。 ここまで分かれば、全体の耐電圧Emaxは下記のようにして求められるのが分かります。 Emax=E1max+E2+E3=E1max(1+C1/C2+C1/C3) …(6) 余談ですが、この問題のように、容量の異なるコンデンサを直列に接続すると、最も容量の少ないコンデンサに電圧が集中します。このことは逆に、同じ容量を接続したつもりでも(コンデンサは一般に抵抗に比べて誤差が大きいので)、容量の少ないものの両端の電圧が高くなってしまうことがある、ということです。 セラミックコンデンサの中には+20%/-80%なんていう誤差のものもありますから、たとえ耐圧50 [V]だからといってこれを直列にして80 [V]かけたら、絶縁破壊するものも出てくる可能性がある、ということです。 耐圧を稼ぐために複数のコンデンサを直列にする時は、容量誤差に注意する必要があります。 それでは、解答に移ります。 題意の数字、E1max=100 [V], C1=10 [μF], C2=20 [μF], C3=50 [μF] をそれぞれ(6)式に代入すれば、 Emax=100×(1+10/20+10/50)=170 [V] となりますので、正解は2と分かります。 | |
 |
 |