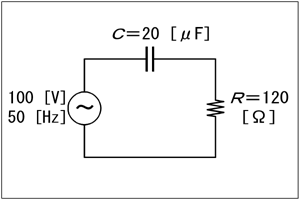
| □ H15年12月期 A-05 Code:[HB0501] : 交流電源に抵抗とリアクタンスからなる回路の有効電力、無効電力、皮相電力等の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
|
交流電源と抵抗だけなら、電源が電池の時と同じオームの法則で解けますが、シリーズにリアクタンス(コンデンサやコイル)が入っているとなると、ちょっとした計算をしなければなりません。また、実はこの問題、強電の分野では非常に基本的な「実効電力」「無効電力」「皮相電力」「力率」といった用語の定義そのものを含んだ問題で、その手の試験を受ける際、あるいは仕事をするには必須の知識です。 原理から説き起こすので、長くなりますが、以下のような順序で説明します。 1.交流で言う「電力」とは何か−「無効電力」「皮相電力」「力率」等を調べる 2.回路の解析−抵抗とリアクタンスからなる回路の電力を解析する という順です。 第1部 交流における「電力」とは何か[1]抵抗は電力を熱に変換するだけの素子直流の時は抵抗Rに流れる電流がIであれば、電力P=I2Rや抵抗両端の電圧Vを使って、P=V2/Rと簡単に求めることができました。これは、抵抗が「流れ込んだ電力を全て熱に変えてしまう」という単純な動作をするからです。コンデンサには直流は流れませんし、コイルは直流的にはショートでした。これが(正弦波)交流になると様相が変わってきます。抵抗は直流の時と同じく、電力を熱に変換するだけの素子なので、P=I2R=V2/R(但し、IやVは実効値)でかまいません。電源の負荷が抵抗のみであれば、流れ出る電流の位相と、かかる電圧の位相にズレはありません。 [2]コイルやコンデンサは電力を蓄えて放出する素子ところが、コイルやコンデンサが入ってくると、電流と電圧の位相にズレが生じてきます。理由を一言で言ってしまうと、「コイルやコンデンサは流れ込んだエネルギーを蓄えて放出する」という動作をするからです。交流ですから、電圧や電流は刻々と変化します。コンデンサは電圧が最大の時に最大のエネルギーを蓄え、コイルは電流が最大の時に最大のエネルギーを蓄える、という動作をします。蓄えたエネルギーはどうするか、というと、各々電圧や電流が小さくなった時に「放出」するのです。放出されたエネルギーは電源側に戻ってきます。このように「蓄えたり放出したり」を繰り返しているだけなので、理想的なコンデンサやコイルは電力を消費しません。ここが交流回路のややこしいところです。[3]戻り電力のために電圧と電流の位相がずれるこの動作を頭の中に思い描いてみると、電源から負荷に向かう電圧・電流の「流れ」はコイルやコンデンサへの「蓄える」方向の電圧・電流と同じですが、さらにこれにこれらの素子が「エネルギーを放出する」方向の電圧・電流が重ね合わさって、電圧と電流の位相がズレてくるのです。[4]電圧と電流の位相がズレている交流に「電力」を定義する | |
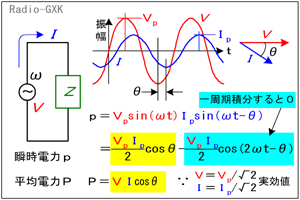 Fig.HB0501_a 電圧と電流の位相ズレ |
例えば、Fig.HB0501_a左のように、電圧V,角周波数ωの交流電源にインピーダンスZの負荷を接続した単純な回路を考えましょう。このインピーダンスは抵抗やコンデンサ、コイルの単体か組合せでできているとしましょう。 電源電圧に対して、電流が角度θだけズレる(図ではIは遅れ側にズレています)とすると、この系で「消費される電力」とは何をもって表されるのでしょうか? それを考えるには、電圧と電流がずれていて、いきなり答えには着けないので、まず、瞬時電力pなるものを考えます。 |
[5]瞬時電力と平均電力これは、ある瞬間に負荷にかかっている電圧と電流を単純にかけたものです。これを1周期分の時間だけ積分して、1周期の時間で割れば、「平均電力」が出る、というわけです。早速計算しますが、三角関数の積を和に直す公式など、ちょっと覚えていない公式を使います。電圧、電流の最大値をそれぞれVp,Ipとすると、 p=Vpsin(ωt)Ipsin(ωt−θ) …(1) =(VpIp/2)cosθ−(VpIp/2)cos(2ωt−θ) …(2) (1)→(2)のところで、 sinθ1sinθ2=(1/2){cos(θ1−θ2)−cos(θ1+θ2)} という公式を使っています。(2)式の第1項(赤字)の項を良く見てみると、時間tが入っていません。θは電圧と電流の位相差で時間に依らず一定ですから、これは定数です。また、第2項(青字)は2ωが入っているので、周波数は倍で変化する項ですが、1周期分積分するとゼロになってしまいます。つまり、pを1周期分積分しても、残るのは第1項だけで、これがそのまま平均電力 P=(VpIp/2)cosθ …(3) なのです。電源が正弦波ですから、電圧、電流の実効値VとIについて、 V=Vp/√2, I=Ip/√2 …(4) ですから、これを(3)に代入して、 P=VIcosθ …(5) となりました。 [6]「皮相電力」「有効電力」「無効電力」「力率」数式ばかりいじっていて疲れたので、ここまでの物理的意味を考えてみましょう。(2)式の第2項は、積分(=1周期の平均)すると消えてしまいました。しかも、電力なのに時間とともに負の値を取り得る、というのはどういうことでしょうか? 実はこれこそが、上で「蓄えたり放出したりを繰り返している」と書いたコイルやコンデンサのエネルギーの流れなのです。蓄えている時は値が正で、戻ってくる時は負になり、平均するとゼロになる、というわけです。 一方、(2)式の第1項は時間に依らず一定しています。位相差θの定義域は、−π≦θ≦πで、式の上では、θ<-π/2やπ/2<θのときにcosθは負になりますが、抵抗やコイルやコンデンサなどの受動部品ではcosθの値が負になることはありません。これが負になるのは負荷として発電機をつないだ時です。 このP(=VIcosθ)こそが、我々が求めたい「電力」すなわち抵抗で熱になる電力で、後に出てくる他の電力と区別して「有効電力」ということがあります。 一方、VIは単に電源電流と電圧を掛けたものです。これを「皮相電力」PSといい、この中には、熱にならない電力も含まれています。これはこの後説明します。 皮相電力と有効電力の比、cosθは「力率」と呼び、1に近いほど電源の出力=消費される電力となり、理想的な状態に近いことを意味します。一方、0に近いほどコンデンサやコイル分から戻ってくる電力の割合が多く、電流が多く流れる割には実際に電力として消費されるのはわずか、ということを意味します。 では、この3種類の電力のお互いの関係は、どうなっているのでしょうか? 第2部 抵抗とリアクタンスからなる回路の電力ここでは、実際の回路で3つの交流電力がどういう関係になっているのかを考えます。[1]素子に流れる電流と両端の電圧はどうなっているか?Fig.HB0501_bのような抵抗R [Ω]とリアクタンスX [Ω]の直列回路を考えます。交流電源は起電力V [V]で周波数はf [Hz](角周波数ωは2πf [rad/s])であるとします。リアクタンスはコイルでもコンデンサでも良く、コイルL [H]ならばX=ωL [Ω]、コンデンサC [F]ならばX=-1/(ωC) [Ω]と置けばよいのです。まず、この回路に流れる電流の大きさI [A]と抵抗の両端に発生する電圧の大きさVR [V]は、それぞれ、 I=V/Z …(6) 但し、Z=√(R2+X2) VR=IR=VR/√(R2+X2) …(7) ここで、R,X,ZはFig.HB0501_bの右上のように、直角三角形の辺の長さで表されるので、(7)式の青字の部分は、 R/√(R2+X2)=R/Z=cosθ …(8) 但しθ=tan-1(X/R) となり、(7)式は、 VR=Vcosθ …(9) と書き換えられます。すると、リアクタンスの両端に発生する電圧の大きさVX [V]は、電流Iが各素子に共通に流れていますから、これまた電圧ベクトルがFig.HB0501_bの右中のように直角三角形を作るので、 VX=Vsinθ …(10) となります。ちなみに、電流ベクトルと抵抗の両端に発生する電圧のベクトルは、同じ向き(すなわち位相が同じ)です。 [2]皮相電力=有効電力+無効電力 なのか? | |
|
各々の素子の電力を見て行きましょう。まず抵抗ですが、電流I [A]はVRと位相が同じなので、消費される電力PR [W]はこれらをそのまま乗ずればよく、(6)式と(9)式から、 PR=IVR=(V2/Z)cosθ =IVcosθ …(11) この式を(5)式と見比べると、全く同じです。つまり、問題に、「抵抗で消費される電力を求めよ」とあれば、有効電力を求めよ、ということだったのです。 では、リアクタンスに「出入り」する電力PX [W]はどうなるでしょうか? |
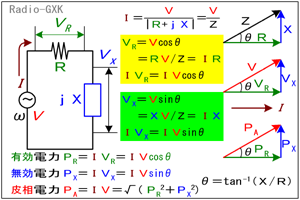 Fig.HB0501_b 電圧ベクトルの直角三角形 |
|
リアクタンス素子の両端に発生する電圧VXと、電流Iの位相が±90°ズレているということは、「熱になる」という有効電力はゼロですが、「蓄えたり放出したり」の電力(無効電力)はゼロではありません。抵抗の時と同様に考えれば、 PX=IVX=(V2/Z)sinθ =IVsinθ …(12) となります。(11)と(12)を見ると、sinとcosの2つの項がありますから、皮相電力PA [W]は、 PA=IV=V2/Z=V2/√(PR2+PX2) …(13) つまり、単純に和を取った 皮相電力=有効電力+無効電力 なのではなく、 PA2=PR2+PX2 …(14) 分かりやすく書けば、皮相電力2=有効電力2+無効電力2だというのです。ここにも、Fig.HB0501_b右下のような「電力の直角三角形」ができました。 [3]直列リアクタンスが複数あったらどうするか上では、リアクタンスが一つの場合を考えていました。リアクタンスは、誘導性(インダクタ、コイル)と容量性(コンデンサ、キャパシタ)の場合があります。これらが複数直列になっていた場合、どう考えたらよいでしょうか? | |
|
Fig.HB0501_cのように、2個のリアクタンスが抵抗に直列に接続されていて、各々容量性リアクタンスX1 [Ω]と誘導性リアクタンスX2 [Ω]であるとします。ここで、リアクタンスは正負、両方の値を取ることに注意して下さい。具体的には、 ・誘導性リアクタンス:X2>0 ・容量性リアクタンス:X1<0 です。 全ての要素が直列に接続されている場合、これらに流れる電流が共通ですから、電流ベクトルと同じ向き(=位相が同じ)の、抵抗の両端の電圧VRを基準(位相0度)に取ることにします。 VRを基準に取ると、容量性リアクタンスX1の両端に発生する電圧Vx1は90度(π/4)遅れます。 |
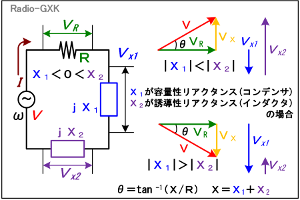 Fig.HB0501_c 複数のリアクタンスの場合 |
|
なので、ベクトル図で描くと、Fig.HB0501_cの右図のように、右向き水平のVRに対してVX1は90度下向きになります。ここで、「あれ、容量(コンデンサ)の位相は進むんじゃなかったっけ?」と思った方は、よく考えて下さい。容量の両端に、ある交流電圧をかければ、それを流れる電流の位相が90度進みます。今は電流(VRの向き)を基準にしているので、電圧は逆に90度遅れ位相、となります。 同様にして、誘導性リアクタンスX2の両端に発生する電圧Vx2はVRに対して90度(π/4)進みますから、VX2は90度上向きになります。 ここまでくれば、後はほとんど[2]と同じです。90度遅れているVx1と90度進んでいるVx2の和Vxを、ベクトルの計算で、 Vx=Vx1+Vx2 …(14) と求めます。実際には|X1|と|X2|の大小関係により、Fig.HB0501_cの右上(|X1|<|X2|)か、右下(|X1|>|X2|)かが決まりますが、どちらも考え方は同じです。 なお、|X1|=|X2|の場合は、両者が「大きさが同じで符号が逆」の場合です。こうなると、Vx1=−Vx2となるので、Vxは(14)式より零となって、抵抗を流れる電流Iは、抵抗値Rと電源電圧Vだけで決まります。これが、直列共振の状態です。 以上で、[2]で考えた、電圧の直角三角形ができましたので、後は電力も同様に考えれば良いわけです。 上記の説明では、VRを基準にしているため、Vx1やVx2がそれぞれ「遅れている」のか「進んでいる」のか、どっちがどっちか、試験中に分からなくなってしまうこともあります。抵抗以外の要素がコイルとコンデンサが各1つである限り、X1とX2はどちらかが正であれば他方は負ですから、ベクトル図から分かるように、どちらが正でも負でも、これら2つのベクトルの和の「長さ」は同じです。 勘のいい方は、(7)式を見てお分かりかもしれませんが、リアクタンスXの項は2乗したものを考えますから、X1やX2のどちらが正でどちらが負でも、和のみが問題となる、Fig.HB0501_cのベクトルVxの「長さ」は同じであり、2乗することで符号は関係なくなります。つまり、ベクトルVxが上を向くか下を向くか(三角形が上向きか下向きか)の違いだけで、ベクトルVの長さは同じ、ということです。 従って、正確なベクトル図が描けなくても、直列回路のコイルとコンデンサでは両端に発生する電圧が180度(π/2)違うんだ、ということが頭に入っていれば、±を間違えても、同じ答えが導き出せます。 [4]力率が悪いと何故いけないか強電の世界では、「力率改善」が課題になっています。力率を改善する、とは、cosθを1に近づけること、すなわち発電所から出て行く電力を全て有効電力にしてしまうことです。ただ、無効電力は「仕事をしない」電力で、出て行ったものが戻ってくるだけなのだから、放っておけばいいような気もしますね。ところがそうは行きません。簡単な例を挙げます。力率が0.5、すなわち、cosθ=0.5(θ=2π/3)の回路があったとします。電気設備などの容量は、皮相電力IVを元にして設計しなければならないので、有効電力を1 [MW]取りたければ、設備容量は2 [MW]ものものを用意しなければなりません。 電力会社は、有効電力にしか電気料金が掛けられないので、やたらと無効電力を「発電所に戻してくる」力率の悪いお客さんは願い下げな訳です。そんなわけで、特にモーターなど(リアクタンス分の多い)力率の悪い負荷を多く使う工場など、大口の顧客に対しては、力率改善設備を導入すれば、電気料金を割引いたりするサービスもある、という訳です。 身近な電気製品で、力率がほとんど1のものは、電熱器を使ったファンヒータ、電気コンロ、白熱電球などだけです。インバータモータが回るエアコンや冷蔵庫、スイッチング電源を多用したテレビやパソコン等はそのままでは力率が悪いため、内部に力率改善用のコンデンサ(進相コンデンサ)や専用回路が入っています。 これでやっと、抵抗とリアクタンスを含む負荷の「電力」は終わりです。 お断りですが、θは絶対値が同じなら正でも負でもcosθの値は同じ(cosθ=cos(-θ))なので、位相が進む、遅れるのどちらに対しても力率は同じ値になります。 また、皮相電力、無効電力の単位を[W]と書きましたが、電力の世界では、それぞれ[VA](ボルトアンペア)、[Var](バール)と呼び分けています。(有効電力はそのまま[W]です。) それでは、解答に移ります。 まず、コンデンサですが、容量C [F]が分かっていますが、リアクタンスX [Ω]が分かりません。そこで、これを求めます。 X=−1/ωC=−159 [Ω] 次に、皮相電力PAは、 PA=V2/Z …(a)(ここでZ=√(R2+X2) [Ω]) 一方、力率cosθは、 cosθ=R/Z …(b) よって、抵抗で消費される電力=有効電力PRは、 PR=PAcosθ=RV2/Z2 電源電圧Vが100 [V]、抵抗Rが120 [Ω]でリアクタンスXが−159 [Ω]をそれぞれ代入して、 PR=120×1002/{1202+(−159)2}=30.2 [W] となりますから、正解は3と分かります。 | |
 |
 |