| □ H17年12月期 A-21 Code:[HH0303] : 100%変調のAM送信機でインピーダンス既知の同軸ケーブルにかかる電圧の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
| |||||||||||
この問題は、給電線の問題というよりはAM変調度と変調波の振幅の問題といった方がいいものです。変調度と振幅の関係の復習から入ります。また、この問題には落とし穴があります。私がハマっただけかも知れませんが…。その説明もしてみます。[1]AM変調度と出力電圧振幅の関係 (よく出るので参考)AM変調の実時間波形と変調度mの関係は、Fig.HH0303_aの右のようになります。変調波振幅のピーク値をa、最小値をbとすると、変調度mは、 | |
|
m=(a−b)/(a+b) …(1) と表せます。また、搬送波の電圧(最大値)をEc、信号波の電圧(最大値)をEsとすると、変調度mは m=Es/Ec …(2) とも表せます。実は、この問題で使うのはこの式だけです。 これらの式の他、AM変調には変調度と電力の関係式もあります。搬送波の出力、すなわち無変調時の出力をPcとすると、変調度がmの時の側波帯の電力をPL(下側)とPU(上側)は、 PL=PU=(m2/4)Pc …(3) |
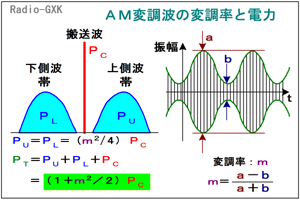 Fig.HH0303_a AM変調波の変調率と電力 |
|
となります。従って全出力PTは、搬送波電力と両側波帯の電力の和ですから、 PT=Pc+PL+PU=(1+m2/2)Pc …(4) となります。 この関係はこの問題を解くのには直接関係はありませんが、AM変調で出題されるかもしれませんので、載せておきました。また、後で「私のやった大間違い」のところでの説明に使用します。 [2]伝送電力とケーブル内の電圧ここでは、ケーブルと負荷は整合が取れている場合について聞かれているので、考慮に入れる必要はありませんが、普通は厳密に整合が取れていないことの方が多いでしょう。整合が取れている場合は、(1)式又は(2)式とオームの法則だけで解けます。まず、同軸ケーブルにかかる搬送波のみの電圧Ec(最大値)を求めます。搬送波電力Pcは、Pc=(Ec/√2)2/Z0 …(5) ですから、これをEcについて解いて、 Ec=√(2PcZ0) …(6) 次に、変調度がmの時は、最大電圧Emaxは(2)式より、 Emax=Ec+Es=Ec+mEc =Ec(1+m) …(7) と表されます。この式に、(6)式から求められるEcを代入すると、 Emax=(1+m)√(2PcZ0) …(8) となるので、問題に与えられた各々の数値を代入すればEmaxが求められます。注意すべきなのは、問題中の電圧が、最大値(信号振幅)で書かれているのか、実効値で書かれているのか、という点です。引っ掛からないようにして下さい。 [3]私のやった大間違い自分の実力を思い知らされる「事件」でした。これは、このページを作成している時のことです。以下に書くことは、私のやらかした大間違いですので、絶対に真似をしないで下さい。変調度がmで、搬送波出力がPcのAM波の出力電力PTが、(4)式で表されることは説明しました。ならば、この電力がZ0の純抵抗に加わったら、その抵抗の両端の電圧がいくらになるか、を計算すればケーブルにかかる最大電圧Emaxが出るじゃないか、と考えたわけです。これが大間違いなのですが、その理由は後で説明します。 PT=(Emax/√2)2/Z0 …(9) なので、これをEmaxについて解いて、 Emax=√(2PTZ0) …(10) これに(4)式を代入して、 Emax=√[2(1+m2/2)PcZ0] …(11) あとは各数値を代入するだけ…というわけなのですが、(8)式と(11)式は似ているようで違います。問題は、どこで考え違いをしているか、です。 正解の方は、単に搬送波振幅と信号波振幅を加えたものから、最大電圧を求めています。一方、「誤解」の方は電力から「実効値」を求め、それを√2倍しています。この考え方は、PTという「正弦波」電力がZ0に消費されている、という前提の下に成り立ちますが、このAM変調波が「正弦波」だと考えたところに誤りがあります。 つまり、AM変調波は「正弦波」ではなく、「ひずみ波」なので、電力とインピーダンスの積の√が振幅に比例する、という関係が成り立たないのです。周波数fcの搬送波を周波数fsの信号波(正弦波)で変調することを考えても、変調されて出てきた信号波、どう見ても正弦波ではありません。便利なオームの法則ですが、交流に適用する場合は、その元となる波形が正弦波なのかどうかに注意を払わないと、大間違いを犯してしまう、という悪例でした。 それでは、解答に移ります。 (8)式に、Pc=100 [W], Z0=50 [Ω], m=1 (100%)を代入すれば、 Emax=2√(2×100×50)=200 [V] となりますので、正解は3と分かります。 | |
 |
 |