| □ H18年08月期 A-06 Code:[HB0402] : LC並列又は直列回路からそのリアクタンスの周波数特性グラフを選ぶ |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||
 Fig.H1808A06a | |||||
この回路は共振回路ですが、単に誘導リアクタンスと容量リアクタンスの並列回路として、全体のリアクタンスを考えてみましょう。[1]誘導性リアクタンスと容量性リアクタンスの並列まず、自己インダクタンスL [H]のコイルのリアクタンスXL [Ω]、容量C [F]のコンデンサの容量性リアクタンスXCはそれぞれ、ω=2πf [rad/s]として、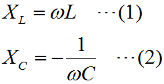 これらの合成インピーダンスZ [Ω]は、 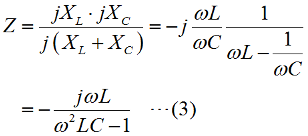 ここで、この並列回路の全体としてのインピーダンスZの虚部(jの係数のこと)をZPとすると、 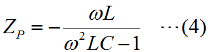 この式から、問題の図のグラフなど想像もつかないのですが、ちょっとした変形をしてみると見通しが開けます。でもこんな計算は、本番でやっていると試験が終わってしまいますので、最後に結果を定性的に説明します。(4)式を部分分数に分解します。 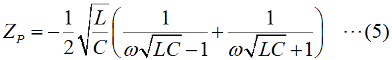 さらにこれを(5)式の()内の部分に着目して、 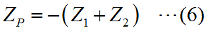 という2つの部分に分ければ各々の項は、 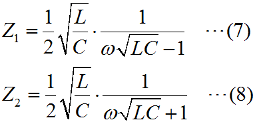 となります。 [2]数学だけで考えると?今、調べたいのはωが変化した時、ZPがどのように振舞うか、です。実際に周波数は0から正の領域で、負の周波数というのはありませんが、一応ここでは単純に数学の議論であるとして、関数の形を探るためにωは全実数を取りうる、として話を進めます。すると、(7)式の分数部分はω=1/√(LC)の時に値が無限大となってしまいます。また、(8)式の分数部分はω=−1/√(LC)の時に値が無限大となります。(7)式と(8)式からZ1やZ2がωの関数と見てグラフを書くと、Fig.HB0402_aのようになります。 | |
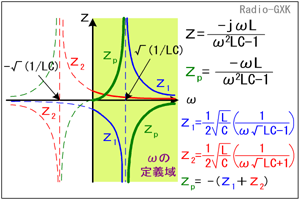 Fig.HB0402_a 並列共振の周波数−リアクタンス特性 |
少しゴチャゴチャしていて見づらいのですが、ここでは、 青い線がZ1 赤い線がZ2 の振舞いを示しています。Z1はωが右側から1/√(LC)に近づく時に+∞、左側から近づく時に−∞に発散します。一方、Z2も同様にωが右側から−1/√(LC)の時に+∞に、左側から近づく時に−∞に発散しています。 ZはZ1とZ2を加えたグラフを、上下ひっくり返したものなので、 緑の線がZp となります。 |
先にも書いたように、試験中にこんな計算をしていたのでは、時間がなくなってしまいます。上の計算は、下の「物理的説明」を補強するためにグラフの形を説明したまでであって、頭の中の理解としては、「数学より物理」「式より現象」ですから、説明が理解できれば、数式は忘れていただいてかまいません。[3]重要なのは「回路としてのどういう動作をする?」ということそれでは、これらについて、回路的な意味を考えます。まず、負の周波数は無いので、0≦ωを定義域とします。ω=0(y切片)では、Z1とZ2は大きさが同じで符号が逆なので、その和はゼロになります。このことは、直流でコイルのインピーダンスがゼロになりますから、実際の現象と合っています。 0<ω<1/√(LC)においては、Zp<0です。この領域では、コイルのリアクタンスが小さく、コンデンサのリアクタンスが大きいので、回路のリアクタンスは誘導性(電源電圧よりも電流が遅れる)となります。 ω=1/√(LC)では、前述(7)式の説明のように±∞に発散します。この点は、この並列共振回路の共振周波数に他なりません。インピーダンスが無限大なので、この回路にこの周波数の交流電源を繋いでも、電流は流れません。 1/√(LC)<ωにおいては、0<Zpです。この領域では、コイルのリアクタンスが大きく、コンデンサのリアクタンスが小さいので、回路のリアクタンスは容量性(電源電圧よりも電流が進む)となります。 [4]誘導性リアクタンスと容量性リアクタンスの直列次に、自己インダクタンスL [H]のコイル容量C [F]のコンデンサを直列にすることを考えます。XLやXCはそれぞれ、(1)式と(2)式で変わりません。これらが直列の合成インピーダンスZ [Ω]は、 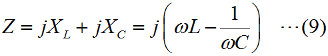 となりますが、(9)式のカッコ内を取り出した、直列のリアクタンス分をZSとすれば、 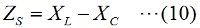 となります。 | |
|
これを周波数特性のグラフにするには、並列の時のように難しくありません。 それが、Fig.HB0402_bです。誘導リアクタンスと容量リアクタンスの和(実際には容量リアクタンスは負なので、実質的には差)を取れば良い、ということになります。 誘導リアクタンスは周波数に比例して大きくなり、容量リアクタンスは周波数ゼロ(直流)で-∞から周波数に反比例して絶対値は小さくなります。 両者を加算した合成インピーダンスはこの図の緑線のように、-∞からZ=0を横切って周波数が高くなるにつれて誘導リアクタンスに漸近します。 |
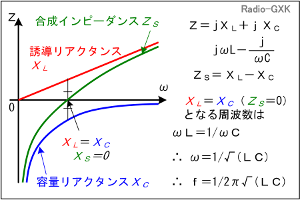 Fig.HB0402_b 直列共振の周波数−リアクタンス特性 |
インピーダンスが零(ZS=0)となる周波数を調べてみると、おなじみの共振周波数の式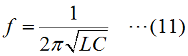 が出てきます。理想的なLC直列共振回路は、共振周波数でインピーダンスでゼロになるので、電流が無限大になる、ということです。 それでは、解答に移ります。 0≦ωの領域で共振点がω=1/√(LC)の1つしかなく、ここでリアクタンスが±∞に発散していて、0<ω<1/√(LC)でリアクタンスが正、かつ、1/√(LC)<ωでリアクタンスが負にあるものは5しかありません。 | |
 |
 |