| □ H18年08月期 A-07 Code:[HC0403] : 電界効果トランジスタの相互コンダクタンスの定義 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
| |||||||||||
FET固有のパラメータである、相互コンダクタンスについて、その定義を問う問題です。FETの動作原理を知っていれば解けますので、まずはFETの基礎的問題で知識を得てからかかると楽でしょう。[1]「コンダクタンス」は抵抗の逆数まずはじめに、「コンダクタンス」はインピーダンス [Ω]やインダクタンス [Ω]に比べて、あまり出てこない用語ですが、単位は[S](シーメンス)で、要するに1/Ωの次元を持つ単位です。抵抗は大きければ大きいほど電流を通しにくいですが、コンダクタンスは大きいほど電流が通りやすい、ということを表します。10 [Ω]=0.1 [S]で、0.05 [Ω]=20 [S]といった具合です。 ところで、なぜ、FETの特性を表すのに、抵抗の逆数なのでしょうか? それは、FETの動作原理である、「電圧で電流を制御する」という機能に由来します。 [2]コンダクタンスは電圧を電流に変換する係数コンダクタンスのことを考える前に、まず、バイポーラトランジスタ(以下、単にトランジスタと書きます)の場合を考えてみます。トランジスタの「(直流)電流増幅率」はhFEで表されます。この意味は、「コレクタ電流の変化分ΔⅠCはベース電流の変化分ΔⅠBの何倍か」、つまりhFE=ΔⅠC/ΔⅠBということです。ここで思い出していただきたいのは、トランジスタは「ベース電流でコレクタ電流を制御する」素子でした。だから、その制御能力を示すものとして、ベース電流からコレクタ電流への変換係数としてhFEが使われるわけです。hFEが大きければ、少ないベース電流の変化で大きなコレクタ電流を変化させられる、というわけです。 それでは、FETではその「変換係数」はどんなものを使ったらよいでしょう? FETは、トランジスタと違い、「ゲート電圧の変化分ΔVGでドレイン電流の変化ΔIDを得る素子」です。ここで、トランジスタと同じように考えれば、ドレイン電流の変化分をゲート電圧の変化分で割れば、ゲート電圧からドレイン電流への変換係数、が出せます。 | |
|
つまり、ΔID/ΔVGがその変換係数に当たります。これが、FETの「相互コンダクタンスgm」ということになります。確かに、電流を電圧で割った形になっていますから、抵抗の逆数の次元を持つ数です。 実際の特性は、Fig.HC0403_aのようになります。図では接合形FETのデプレッション形の特性を挙げていますが、MOS形(デプレッション・エンハンスメント)でも本質は変わりません。 ここで注意しなければならないのは、第一には、この曲線はドレイン-ソース間電圧VDSを一定にして測定しなければならない、ということです。 |
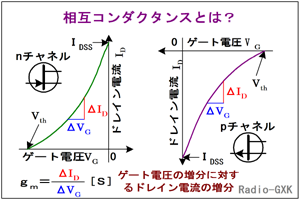 Fig.HC0403_a 相互コンダクタンスとは |
|
VDSが異なると、曲線の形も違ってきます。また、第2点は、ゲート電圧によって曲線の傾きが変わるので、たとえVDSが一定でも、gmはVGに対して一定値ではない、ということです。グラフの曲線の傾きは、場所によって違います。まぁこれは、増幅器を設計する際に必要な知識なので、試験には出ませんが。 相互コンダクタンスが大きい、ということは、小さなゲート電圧の変化で、大きなドレイン電流の変化を得ることができる、ということであり、FETの特性を表す数値になっていることは理解できるかと思います。 接合形FETの特性が出たついでに、ⅠDSSについて調べておきましょう。デプレッション接合形の場合、ゲートはチャネルに対して逆バイアスをかけて使用しますから、Nチャネルの場合ゲート電圧(ソースが基準)は0 [V]より大きな電圧は掛けられません。この(VG=0 [V])ときに流れるドレイン電流が最大となります。この電流値をⅠDSSといい、FETのもう一つの特性値になっています。ⅠDSSは、製造に起因するバラツキが大きく、ちょうどトランジスタのhFEのように、その値でランク分けされていることがあります。実回路の設計では、このバラツキにも注意しなければなりません。 それでは、解答に移ります。 ここまででVGと書いているものは、ゲートソース間電圧です。問題文から、上記の内容とgmの選択肢を比べれば、ゲート電圧の変化分に対してドレイン電流の変化分を示している、1が正解と分かります。 以下、インチキ解答法?ですが、コンダクタンス(=1/Ω)の次元を持つ選択肢は1と3しかありません。残りの単位はみなΩです。5択の問題が、いきなり2択の問題になってしまいました。このあたりも、うっかりミスを防ぐコツです。 | |
 |
 |