周波数カウンタの動作原理基準時間発生部ゲート回路計数回路表示部 1カウント誤差非同期 - １アマの無線工学 H18年12月期 A-24

□ H18年12月期 A-24 Code:[HJ0801] : 周波数カウンタのブロック図と動作原理

検索サイトから来た方は…
無線工学の基礎トップへ

以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます

■ 無線工学を学ぶ

(1) 無線工学の基礎

年度別出題一覧

H11年 4月期,8月期,12月期

H12年 4月期,8月期,12月期

H13年 4月期,8月期,12月期

H14年 4月期,8月期,12月期

H15年 4月期,8月期,12月期

H16年 4月期,8月期,12月期

H17年 4月期,8月期,12月期

H18年 4月期,8月期,12月期

H19年 4月期,8月期,12月期

H20年 4月期,8月期,12月期

H21年 4月期,8月期,12月期

H22年 4月期,8月期,12月期

H23年 4月期,8月期,12月期

H24年 4月期,8月期,12月期

H25年 4月期,8月期,12月期

H26年 4月期,8月期,12月期

H27年 4月期,8月期,12月期

H28年 4月期,8月期,12月期

H29年 4月期,8月期,12月期

H30年 4月期,8月期,12月期

R01年 4月期,8月期,12月期

R02年 4月期,9月期,12月期

R03年 4月期,9月期,12月期

R04年 4月期,8月期,12月期

分野別出題一覧

A 電気物理, B 電気回路

C 能動素子, D 電子回路

E 送信機, F 受信機

G 電源, H アンテナ&給電線

I 電波伝搬, J 計測

■ サイトポリシー

■ サイトマップ[1ama]

■ リンクと資料

■ メールは下記まで

2022年

12/31 12月期問題頁掲載

09/01 08月期問題頁掲載

05/14 04月期問題頁掲載

H1812A24 Counter

無線工学 > １アマ > H18年12月期 > A-24
A-24	次の記述は、図に示す計数式周波数計（周波数カウンタ）の動作原理について述べたものである。［　］内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、［　］内の同じ記号は、同じ字句を示す。

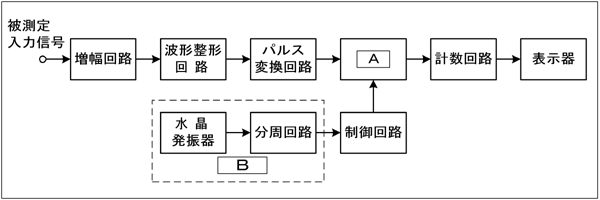問題図（横長） H1812A24a

Fig.H1812A24a

(1)	被測定入力信号は、同一周波数のパルス列に変換され、一定時間だけ開いた［Ａ］を通過するパルスが計数回路で数えられ、その数値が直接周波数として表示されるものである。
(2)	水晶発振器と分周回路による［Ｂ］で正確なＴ [秒]周期でパルスが作られ、制御回路への入力となる。Ｔが１ [秒]のときは、計数回路でのカウント数がそのまま周波数[Hz]の表示となる。
(3)	測定誤差としては、水晶発振器の確度による誤差のほか、制御回路の出力信号と通過パルスの時間的位置関係から生ずる［Ｃ］誤差などがある。

	Ａ	Ｂ	Ｃ
１	ゲート回路	基準時間発生部	±１カウント
２	ゲート回路	周波数変換部	トリガ
３	ゲート回路	基準時間発生部	トリガ
４	トリガ回路	周波数変換部	トリガ
５	トリガ回路	基準時間発生部	±１カウント

周波数カウンタの構成と動作が問題です。この計測器のミソは、入力信号をパルスに変換するところと、一定時間だけ開いているゲートを通り抜けたパルス数を数える部分です。［１］周波数カウンタの構成と動作原理　構成は、問題図でほとんど完結しているので、これを元に説明します。入力をパルスに変換する周波数カウンタを繋ごうというのですから、入力は周波数を知りたい何らかの周期波形であることでしょうが、波形がどんなものか、あるいは電流を流し出せるほどインピーダンスが低くない信号源であることも考えられます。そこで、入力をバッファで受けて、波形整形してデジタル信号（パルス信号）に変換します。これが、問題図で入力からパルス変換回路までの働きです。正確な時間基準を発生させる周波数カウンタとは、単位時間あたり、何発のパルスが入ったか、を数える装置なので、その「単位時間」に相当する正確な時間が測れなければなりません。周波数カウンタでは、通常、TCXO（温度補正水晶発振器）等の正確な発振器と、分周比が可変な分周回路で時間基準を発生させます。一定時間の間だけパルスを通す単に「ゲート」といっても良いでしょう。上で発生させた正確な時間基準に基づいて、その間に到来した入力パルスのみを通します。ゲートはまさにその「門」となる回路です。入力パルスは、もちろん、入力信号を整形したものです。パルス数をカウントするゲートを通ったパルスの数を数えます。高速にカウントしなければならないので、ソフトウェアで数えるのではなく、専用のハードウェア（ロジック回路で組んだカウンタ）でカウントします。次のカウント動作を始める前にゼロにリセットします。結果を表示するカウンタの出力を液晶（LCD）やLEDの表示器に表示させます。上記の動作に従って、例えば、ゲートが0.1 [s]開いている間に１万発のパルスが入ってきたら、100,000 [Hz]と表示させるわけです。ゲートの時間を変えるには、水晶発振器の後にある、可変分周器の分周比を変化させます。　実際の周波数カウンタは、トリガレベル（パルス１発とカウントするスレッショルドレベル）の調整や、ゲートタイムの切替等、他の付属機能がたくさん付いていますが、本質的な部分を抜き出せば、問題図のようになります。［２］１カウント誤差について　選択肢の中に、「±１カウント誤差」というものが出てきます。これについて簡単に説明します。
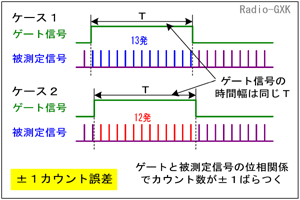Fig.HJ0801_a ±１カウント誤差の発生原理	Fig.HJ0801_aのように、入力が一定間隔ｔ [s]で入ってくる時、パルスのｎ発に要する時間(ｎ-1)ｔ [s]が、ゲートが開いている時間Ｔ [s]に比べてわずかに短いとします。　入力信号と、周波数カウンタ内部の水晶発振器内部のクロックは「非同期」ですから、その位相差は一定とは限りません。　つまり、両者の位相差によっては、ゲートの中にｎ発入る時と、ｎ－1発しか入らない時とがランダムに発生して、最下位桁の表示がコロコロ変わります（図で言うと、13発入る時と12発しか入らない場合がある）。
このように、被測定信号とカウンタ内部のクロックの位相差による測定値のばらつきを、(±)１カウント誤差、といいます。入力信号のレベルが小さく、S/Nが悪いような信号では、波形整形する時に振幅方向の揺らぎ（＝ノイズ）が時間方向の揺らぎ（ジッター）に変換されて、最下位の桁がコロコロ変わることもありますが、これは±１カウント誤差とは言いません。　また、水晶発振器の精度や確度そのものが低ければ、これももちろん誤差になります。・ここで、精度と確度について… 　水晶発振器でいうと、発振周波数が真の周波数にどれだけ近いか、が「確度」で、カウンタに表示された値が（変動しないとすれば）どれだけ真の周波数に近い値を示しているかを表すものです。一方、入力の周波数が全くぶれていない時に、水晶発振器が原因（発振周波数のふらつき）で表示がぶれる程度を「精度」といいます。　従って、確度は高くても精度が低い（表示がコロコロ変化するような）周波数カウンタも、理屈上は存在することになります。機種を選定する時は、両方を考慮に入れて選ばなければなりません。それでは、解答に移ります。　Ａ…ここは基準時間信号で被測定パルスを通過させるゲート回路です　Ｂ…ここではゲートを開く基準時間を発生させるので、基準信号発生部です　Ｃ…信号とゲートの位相が原因で生じる誤差は±１カウント誤差ですとなりますから、正解は１と分かります。