| □ H19年04月期 B-04 Code:[HI0402] : 等価地球半径の考え方 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
|
大気の屈折率は高さにより変化し、上層に行くほど屈折率が[ア]なる。そのため電波の通路は[イ]に曲げられる。しかし、電波の伝わり方を考えるとき、電波は[ウ]するものとして取り扱った方が便利である。このため、地球の半径を実際より[エ]した仮想の地球を考え、この半径と実際の地球の半径との比を等価地球半径係数といい、これを通常Kで表し、Kの値は[オ]である。 | |||||||||||
| |||||||||||
常識では、光や電波はまっすぐ飛ぶ、と考えますが、それは一様な媒質の中を伝搬する場合であって、地上の大気のように、高さ方向に屈折率が一様ではない物質の中では光は曲がります。曲がっていては考えにくいので、地球の半径が変化した「ことにして」考えれば、電波の経路が直線だと考えても良い、というのが「等価地球半径」の考え方です。[1]電波や光は曲がって進む? 屈折率の変化と電磁波の経路光と電波は、周波数が違うだけで、同じ電磁波ですので、ここでの説明では学校でやった(かも知れない)光の屈折の実験例で説明します。 | |
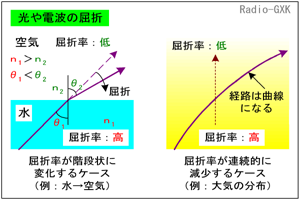 Fig.HI0402_a 屈折率の変化と電磁波の伝搬 |
まず、屈折率がある表面で突然、階段状に変化する場合を考えます。Fig.HI0402_aの左がその図ですが、例えば、水の中を進行してきたレーザー光が、空気中に出るような場合です。水の方が屈折率が高く、空気の方が低い状態です。 この場合、光は水面に近づく方に曲がります。つまり、屈折率の高い方から低い方に電磁波が進行する場合、進行方向は屈折率の高い方に曲がります。これを、スネルの法則と言って、水の中に箸を入れると、箸が曲がって見える、あの現象の説明です。 |
|
この法則を定量的に表せば、証明は行ないませんが、2つの媒質の屈折率をn1とn2、及び界面の法線と光線の進行方向がなす角をθ1とθ2とすると、 n1sinθ1=n2sinθ2 …(1) という関係になります。この式から、n1>n2ならθ1<θ2であることがわかります。 では、屈折率が連続的に変化しているような媒質では、経路はどうなるでしょうか? このようなケースは、地球の大気が地表から上空に向かって、屈折率がほぼ直線的に減少している状態(Fig.HI0402_a右)があてはまります。 考え方としては、大気が、厚みの薄い多数の膜のような層からなっていると考え、それらの屈折率がn1>n2>n3>…>niと、わずかずつ上空方向に向かって減少してゆく状態をイメージすればよいです。つまり徐々に屈折率が減少するi層の多層膜が重なっている、ということです。 スネルの法則に依れば、光の経路は、層を一つまたぐたびに、わずかにこの図の下方に曲げられます。従って、大気中の光の光跡は直線にはならず、斜めに打ち上げても、地面方向に曲がることになります。さらに、大気の屈折率分布自体が同心円(球?)状なので、事情は複雑ですが、光跡が地面に向かって曲げられることには変わりありません。 [2]電波の経路を直線で表したい打ち上げた電波の経路が、地面方向に曲げられることは分かりましたが、実際TVやFMの送信所を建設する場合など、カバーエリア(受信可能な範囲)を設定し、鉄塔の高さやアンテナの垂直面内の指向性・利得を決めたいのに、「電波が曲がって飛ぶ」のでは設計しづらくて仕方ありません。 | |
|
例えば、山のない砂漠のような平原に、水平面内が無指向性のアンテナを建てて四方を見回したとしましょう。電波が(光も)真の直線で飛ぶなら、アンテナのある高さから見た水平線までが「見通し距離」で、それより向こう側は直接波は届かないはずです。 しかし、実際には地図上で描いた「見通し」距離よりも遠くに届きます。これは、Fig.HI0402_bの左のように、電波が実際には地表方向に曲げられて飛ぶためで、いわば、地球の丸みの向こう側に回り込んでいる、というイメージです。 |
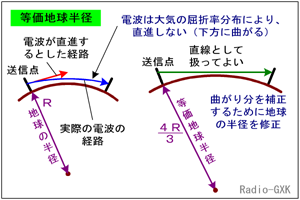 Fig.HI0402_b 幾何学的経路と実際の経路 |
|
これでは、途中の障害物などが実際に経路にかかるのかどうか分からないので、電波が直線で飛ぶと考える「代わり」に、地球の半径が大きくなった、と考えたらどうだろう、という発想の転換をしたのがFig.HI0402_bの右になります。 実際、このような仮定(電波の経路を直線にするには地球の半径を変えればよい)が成り立つのか、の証明は(私もちゃんと説明できない=分かってない、ので)でできませんが、数式だけを追って行くと、確かにそう考えて差し支えありません。 [3]等価地球半径を計算する等価半径を考えるには、先に述べたように、大気も球状に屈折率分布をしているので、その影響を考慮した「修正屈折率」というものを使います。詳細は上級(プロ)の資格の範囲になりますので省きますが、ここから「実際の地球の半径Rの4/3倍が等価地球半径」という結論が出ます。つまり、地球の半径が4/3倍になったと考えれば、電波の経路は直線で考えてよい、ということです。 それでは、解答に移ります。 ア…大気は上層に行くほど屈折率が1小さくなります イ…上層ほど低い屈折率分布の中では、電波は5下方に曲げられます ウ…電波は10直進するものとして扱うと便利です エ…電波が直進すると考えるには、地球が2大きくなった、と考えます オ…その大きくなる倍率がKで、通常の大気ではK=8 4/3です となります。 | |
 |
 |