コンデンサ合成容量並列スイッチ電荷保存則かかる電圧 - １アマの無線工学 H19年08月期 A-01

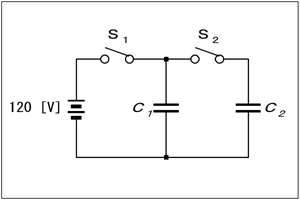
□ H19年08月期 A-01 Code:[HA0301] : ２個の並列コンデンサとスイッチ回路。スイッチ切替前後で電荷量保存則を用いた計算

検索サイトから来た方は…
無線工学の基礎トップへ

以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます

■ 無線工学を学ぶ

(1) 無線工学の基礎

年度別出題一覧

H11年 4月期,8月期,12月期

H12年 4月期,8月期,12月期

H13年 4月期,8月期,12月期

H14年 4月期,8月期,12月期

H15年 4月期,8月期,12月期

H16年 4月期,8月期,12月期

H17年 4月期,8月期,12月期

H18年 4月期,8月期,12月期

H19年 4月期,8月期,12月期

H20年 4月期,8月期,12月期

H21年 4月期,8月期,12月期

H22年 4月期,8月期,12月期

H23年 4月期,8月期,12月期

H24年 4月期,8月期,12月期

H25年 4月期,8月期,12月期

H26年 4月期,8月期,12月期

H27年 4月期,8月期,12月期

H28年 4月期,8月期,12月期

H29年 4月期,8月期,12月期

H30年 4月期,8月期,12月期

R01年 4月期,8月期,12月期

R02年 4月期,9月期,12月期

R03年 4月期,9月期,12月期

R04年 4月期,8月期,12月期

R05年 4月期,8月期,12月期

R06年 4月期,8月期,12月期

分野別出題一覧

A 電気物理, B 電気回路

C 能動素子, D 電子回路

E 送信機, F 受信機

G 電源, H アンテナ&給電線

I 電波伝搬, J 計測

■ サイトポリシー

■ サイトマップ[1ama]

■ リンクと資料

■ メールは下記まで

2025年

03/31 R06/12月期問題頁掲載

03/31 R06/08月期問題頁掲載

03/31 R06/04月期問題頁掲載

03/31 R05/12月期問題頁掲載

03/31 R05/08月期問題頁掲載

03/31 R05/04月期問題頁掲載

H1908A01 Counter

無線工学 > １アマ > H19年08月期 > A-01

A-01

次に示す回路において、最初スイッチＳ₁及びスイッチＳ₂は開いた状態にあり、コンデンサＣ₁及びコンデンサＣ₂に電荷は蓄えられていなかった。次にＳ₂を開いたままＳ₁を閉じてＣ₁を120 [V]の電圧で充電し、更に、Ｓ₁を開きＳ₂を閉じたとき、Ｃ₂の端子電圧が90 [V]になった。Ｃ₁の静電容量が3 [μF]のとき、Ｃ₂の静電容量の値として、正しいものを下の番号から選べ。

１	1 [μF]
２	2 [μF]
３	3 [μF]
４	4 [μF]

問題図 H1908A01a

Fig.H1908A01a

この問題を解くには、電荷量の保存則を使います。最初にＳ₁をONにして充電し、これをOFFにした以降は、Ｓ₂をONにする前後で電荷の総量は変わらない、という理屈を使って解きます。［１］電荷量保存則とは何か？　「電荷量保存則」と聞くと、「ああ、また物理の難しい法則か。もう『何とかの保存則』と聞くだけで嫌だな」と思われる方も居られるでしょう。大体、言葉が難しくていけません。法律用語みたいです。　ただ、言っている内容は簡単なので、法則の名前がどうのこうのよりも、その意味するところだけを理解してしまえば、アレルギーも解消すると思います。　電荷は物理的には、負電荷＝電子が（中性状態より）多い状態、正電荷＝電子が少ない状態、なので、電子がどこかに消えたり、どこからともなく湧き出したりしない限り、最初に分かっていた電荷量はどこにどう蓄えられようが、変化しないはずです。この問題では、ここに着目します。［２］電荷量保存則を水の量で考える　まず、Ｃ₁を容量が既知のコンデンサ、Ｃ₂を容量が不明のコンデンサとします。また、最初にＣ₁に印加した電圧をＶ₀とします。
ここでは、Fig.HA0301_aのように考えます。つまり、底面積（＝静電容量）のわかった入れ物Ｃ₁と、底面積が不明の入れ物Ｃ₂です。また、電荷量は水の量で、コンデンサの両端の電極の電圧は水位の高さであらわすものとします。（両者を繋ぐ管の中の水の量は無視します。）　着目すべきなのは、スイッチＳを入れたあと、Ｃ₁とＣ₂は、並列接続状態となる、ということと、スイッチＳを入れる前後で電荷（＝水）の量は変わらない、ということです。この容器の例では、並列接続により底面積が増えたことになります。　そのような入れ物を繋いで、中央の栓Ｓを開ければ、両者の水位（＝電圧Ｖ₁）が等しくなるところまでＣ₁からＣ₂へ水が流れ込み、安定します。栓を開けた前後で、水の全体量は変わりません。　こう考えてくると、電荷が保存されることが容易に以下の式で表されます。　Ｃ₁・Ｖ₀＝(Ｃ₁＋Ｃ₂)・Ｖ₁　…(1) となりますから、これを変形して未知の容量Ｃ₂について解けば、　Ｃ₁・(Ｖ₀/Ｖ₁)＝Ｃ₁＋Ｃ₂　…(2) 　∴ Ｃ₂＝(Ｖ₀/Ｖ₁－1)・Ｃ₁　…(3)	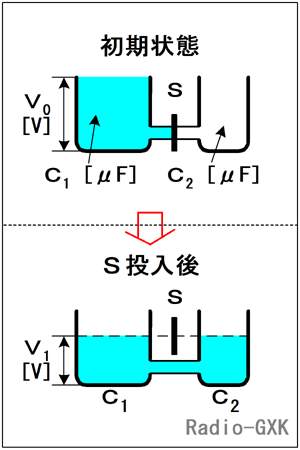Fig.HA0301_a 電荷量保存則
と求められます。それでは解答に移ります。　(3)式に題意の数値（Ｃ₁＝3 [μF]、Ｖ₀＝120 [V]、Ｖ₁＝90 [V]）を代入すれば、　Ｃ₂＝3×(120/90－1)＝1 [μF] となりますから、正解は１と分かります。　暗算で出すとすれば、「スイッチＳ₂をON後に電圧が3/4だから、Ｃ₁とＣ₂の合成容量がＣ₁の4/3倍。ということはＣ₂はＣ₁の1/3の容量！」ということで、回路をいじったことのある方なら、ここに挙げた計算は不要かもしれません。(3)式のちょっとした計算が必要になりますが。いずれにしても、電気回路の基礎的問題なので、確実に正解したい問題です。