| □ H19年08月期 A-12 Code:[HE0603] : デジタル伝送系のブロック構成と動作原理の説明 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
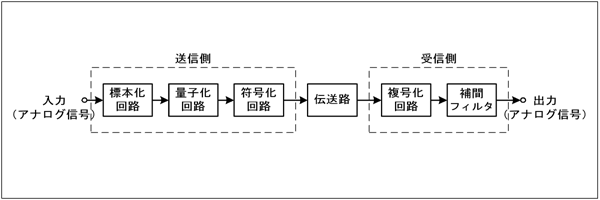 Fig.H1908A12a | ||||||||||||||||||||||||||
| ||||||||||||||||||||||||||
|
アナログ信号をデジタル化し、伝送・記憶・処理する方式は、昔からあるCDをはじめ、いまやデジカメ、携帯電話、光ファイバに至るまで、ほとんどの電気信号で用いられています。この問題では、その最も基礎の部分である、アナログ信号をデジタル化する部分について問われています。アマチュア無線は、どちらかというとずっとアナログな世界で運用されてきました。そのため、デジタル・パルスと聞くといいイメージをお持ちでない方も居られるでしょうが、通信方式として狭帯域化や高速化が図れることで注目されているわけですから、先進技術の一端として知っておくのも悪くはないのではないでしょうか? 送信側では、アナログ信号をデジタル化し、搬送波にデジタル変調をかけて電波に乗せます。受信側では、受けた電波からデジタル信号を取り出し、アナログ信号に戻します。順を追って見て行きます。 [1]アナログ信号をデジタル化する方法…その1 標本化アナログ信号は、「時間」とともに「振幅」が無段階に変化する電気信号です。これを「デジタル化する」というのはどういうことでしょうか? 「デジタル信号」というのは「飛び飛びの」時間、や振幅で表現された信号です。アナログ信号をデジタル信号に変換することを考えるためには、その「時間」と「振幅」に分けて考えます。 | |
|
Fig.HE0603_a左のようなアナログ信号があったとします。時間的に、波打つような変化をしている信号で、途中で値が突然飛んだり消えたりはしないものとします(世の中にそういう信号がないわけではないですが、ここでは音声を考えます)。 この値を「サンプル&ホールド回路」という、ちょっと変わった回路で処理します。この回路は、外部からアナログ信号とクロックが入力されていて、クロックが入力された瞬間のアナログ信号の値を「掴んで(サンプリング=標本化)」次のクロックが入るまで「保持して(ホールド)」おく、という回路です。 |
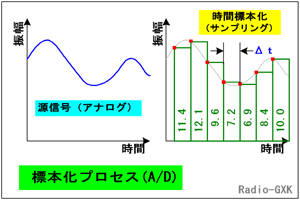 Fig.HE0603_a 時間軸方向に飛び飛びにする…標本化 |
|
ですから、サンプル・ホールド回路の出力は、Fig.HE0603_aの右のようになります。ここで、クロックが一定間隔で入力されているとすると、この棒グラフの幅は全て等しくなります。このような信号処理のことを(時間)標本化あるいは(時間)サンプリングする、といいます。言い換えれば、まず「時間的にデジタル化」するわけです。このクロックの周波数を、「標本化(あるいはサンプリング)周波数」といい、ここではfsと書くことにします。この周波数fsが高ければ高いほど、元の波形が急激な変化をして(高い周波数成分を含んでいて)も後にアナログ信号に戻す時に波形が忠実に復元できることになります。 ところで、「あるサンプリングが行なわれた瞬間と、次のサンプリングの瞬間の間に変化した信号は再現できないのでは?」と思います。その通りで、再現できません。とりもなおさずそのことは、上で述べた「高い周波数成分を含む」信号、ということになるので、標本化周波数を上げなければなりません。それで、再生側で信号が復元できるのか、どの程度までfsを上げればよいのかについては、最後に書きます。 [2]アナログ信号をデジタル化する方法…その2 量子化時間的には飛び飛びの信号になりました。続いて、振幅方向にも飛び飛びの値に変換しなくてはなりません。 | |
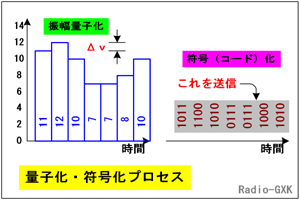 Fig.HE0603_b 振幅方向に飛び飛びにする…量子化 |
Fig.HE0603_aの右のグラフで、棒の下に数値が入っていますが、その数値が時間サンプリングされた電圧 [V]だとします。これを今、0〜15 [V]の1 [V]きざみで16段階の値に四捨五入で「丸めて」しまいます。 するとその結果は、Fig.HE0603_b左のようになります。このようにある値Δv(ここではΔv=1 [V])を単位として、その値に満たない端数を丸め(大概は四捨五入)て、信号がΔvの何倍になるかを求める処理を「量子化」といいます。「量子」と聞くと物理をやったことのある方は、粒子が壁を通り抜ける「量子力学」を思い浮かべますが、電気信号の量子化はもっとイメージ的には直感的で簡単です。 |
|
「何倍になるか」を求めた上に、小数点以下は四捨五入してしまいますから、結果は必ず整数です。こうなれば、アナログ信号が一定の時間間隔で出てくる「数字」(=データ)になってしまったので、もうデジタルの世界で処理できます。今回はΔv=1 [V]としていますから、0〜15 [V]までの値は4 [bit]で表現できます。 実際のA/Dコンバータでは、±2.5 [V]を16 [bit]で表現したりしますから、その場合はΔv=5 [V]/216=76.3 [μV]という、非常に細かな値になります。 一般に、n [bit]で表現できる「段階数」は、2nとなりますから、8 [bit]で256、12 [bit]で4096、16 [bit]で65536、というように、ビット数が増えれば増えるほど、細かさは「指数関数」そのもので細かくなってゆきます。入力の何 [V]をフルスケールにするか、は個々のコンバータの仕様に依存します。 さて、これで「時間標本化」と「振幅量子化」という二つのデジタル化が完了しました。振幅の量子化で得られたデジタル値を、その値を表現する形式に変換することを符号化(又はコード化)といいます。「値を表現する形式に変換」というのは抽象的ですが、この図の例で言えば、12→1100、7→0111というような10進数を2進数に変換することです。このような一連のデジタル化信号処理をPCM (Pulse Code Modulatuin)といいます。 ここで出てきたデジタルデータを、通信で他の場所に送る場合、どの程度の伝送速度(「ビットレート」とも言います)B [bit/s]が必要になるかを考えてみましょう。答えは案外簡単で、サンプリング周波数fsの時間間隔で、n [bit]のデータが続々と出てくるわけですから、単位時間に出てくるデジタルデータのビット数(すなわち伝送速度B)は、 B=nfs [bit/s] …(1) となります([bit/s]は[bps]とも書きます)。例えば、モノラルのCD音質(fs=44.1 [kHz]、n=16 [bit])であれば、44.1 [kHz]×16 [bit]=705.6 [kbit/s]となり、電話音質(fs=8 [kHz]、n=8 [bit])であれば、8 [kHz]×8 [bit]=64 [kbit/s]ということになります。普通は、このままで伝送すると非常にデータ量が多くなるので、人間の目や耳で知覚できない情報を(デジタル的に)削除するなどの「圧縮」を加えて伝送します。デジカメで使うjpeg形式も、メモリープレーヤーに録音する時のmp3形式も、みな圧縮された情報のフォーマット名です。 [3]デジタル信号をアナログ化する方法…その1 D/A変換受信側で復調されたデジタル信号を、アナログ化する方法の第1は、1と0の数字の羅列であるデジタル信号を、電気信号の電圧振幅または電流量に変換することです。もう少し詳しく言うと、復調されたデジタル信号は、通常1ビットだけでは意味を持たないので、8ビットや16ビットといった、ある「まとまり」をひとつの単位として、その単位が持つ量を電流や電圧に変換する、という意味です。 | |
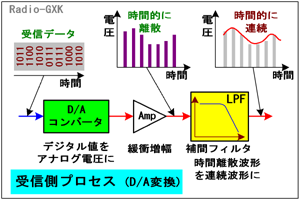 Fig.HE0603_c 受信側での信号処理 |
D/A変換の具体的なイメージを持っていただくために、簡単な4ビットのD/Aコンバータを考えます。4ビットのデジタル値を入れると、0〜1.5 [V]の電圧を出力するコンバータです。 このコンバータにいろいろなデジタル値を入力した時に、出力がどうなるかを見てみると、 0000 … 0 [V] 0001 … 0.1 [V] 0010 … 0.2 [V] : 1110 … 1.4 [V] 1111 … 1.5 [V] |
|
というようになります。このD/Aコンバータが、データが次々に送られてくるたびに、その値に応じた電圧を出力すれば、元の波形に「近い」階段状の波形が得られることが分かります。また、ビット数が多いほど、この電圧の「刻み」が細かくなりますし、データの切り替えを高速にすれば、高い周波数でも再現できそうだ、ということが定性的に分かります。 その概念を示したのがFig.HE0603_cの主に左半分です。ここでは、4ビットのD/A変換器と次段へのバッファアンプ(緩衝増幅)を一体と考えていますが、それよりも本質的なのは、上に書いたような機能によって、0と1信号の信号を電圧(又は電流)量に変換する機能が、D/A変換である、ということです。 ところが、ここではまだ時間的には離散(階段状)信号です。この図では、時間離散の信号を棒グラフのような信号で書いていますが、理想的には非常に鋭いパルスになります。実際のD/A変換器は次のデジタル値が入るまで、一定レベルを保ち続けるので、「棒グラフ」そのものになります。(このことはD/A変換においてはあまり本質的ではありませんが、後に述べるフィルタの設計が少し違ってきます。) いずれにせよ、ここではまだ振幅も離散的ですし、時間方向も離散的です。これを元の波形に近い滑らかなアナログ信号に直すには、次段のフィルタを通さなくてはなりません。 [4]デジタル信号をアナログ化する方法…その2 補間フィルタD/A変換器で得られた「階段状」の波形を、滑らかなアナログ信号に直すには、補間フィルタをD/A系の後段に設けます。「補間」と名がついていますが、中身はローパスフィルタ(低域フィルタ)で、階段状の波形の「角を取る」働きをします。厳密にはいろいろ理論的な考察はありますが、A/Dコンバータのサンプリング周波数(=D/Aの変換周波数)をfsとすると、このフィルタのカットオフ周波数はfsより低くなければなりません。また、フィルタの「切れ」は鋭いほど良いのですが、実際には帯域内のリプルや遅延特性とのトレードオフになりますから、「そこそこ」で設計されています。 要するにこの低域フィルタは、「階段波形」の角を丸め、元のアナログ信号に極力近い滑らかな信号にしてやる働きをするフィルタ、ということです。 それでは、解答に移ります。 A…「標本化」とはアナログ信号を一定の時間間隔で離散化することです B…量子化ビット数が多いほど1ステップが小さく、量子化雑音は減少します C…補間フィルタに用いるのは低域フィルタ(LPF)です となりますから、正解は2と分かります。 | |
 |
 |