| □ H19年08月期 A-15 Code:[HD0503] : AM受信機に用いられる2乗検波の特徴・動作の説明 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||
| |||||||||
AM波の検波方式には様々なものがありますが、その中に二乗検波というものがあります。これはダイオードに入る信号レベルが小さい時の出力が、入力の二乗に比例する部分を利用するものです。出力が入力に比例しませんので、様々な課題があります。[1]二乗検波の原理Fig.HD0503_a右下に検波回路を示します。これだけではただの検波回路ですから、直線検波回路なのか二乗検波なのか分かりません。 | |
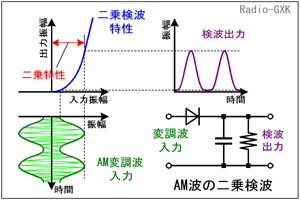 Fig.HD0503_a 二乗検波の動作原理 |
二乗検波というのは、この検波回路に使われているダイオードの特性(Fig.HD0503_a左上)を利用するものです。ダイオードの入力振幅が小さい時は、出力が入力の二乗に比例するような領域があります。 高周波増幅段などの利得の設定で、この領域の振幅が検波器に入るようにしておけば、高周波入力(の包絡線)振幅の二乗に比例した検波出力が得られるはずです。 お気づきかもしれませんが、「出力が入力の2次関数」になったら、出力が歪んでしまわないか? という疑問がわきます。 |
歪みの発生と、その歪みをどう処理するかは、この後に書きます。[2]二乗検波すると二次高調波が出てくるダイオードの入出力特性を出力=入力に比例する項+入力の二乗に比例する項 だとして、AM変調波(変調度m、搬送波周波数ω、被変調信号周波数φ)をこの系に入力すると、周波数が低い順に以下の成分が出力されます。 (0) 直流分 (1) 被変調信号(mcosφtに比例) (2) 被変調信号の二乗成分(m2cos2φtに比例) (3) 下側波帯(msin(ω−φ)tに比例) (4) 搬送波(sinωtに比例) (5) 上側波帯(msin(ω+φ)tに比例) (6-1) 周波数2倍の下側波帯(m2cos{(2ω−2φ)t}に比例) (6-2) 周波数2倍の下側波帯(m2cos{(2ω−φ)t}に比例) (7) 搬送波の2倍波(cos2ωtに比例) (8-1) 周波数2倍の上側波帯(m2cos{(2ω+φ)t}に比例) (8-2) 周波数2倍の下側波帯(m2cos{(2ω+2φ)t}に比例) 式で書くと大変なことになるので、言葉で書いていますが、実はこれが平滑コンデンサを通すと簡単になります。 それは、高周波(角速度の部分がωや2ωを含む)成分は、平滑コンデンサを流れて出力には出てきませんから、(3)以降は出力には出てきません。(0)の直流分はあってもなくてもかまいません(後段の増幅回路をACカップリングにするなどしてカットできる)し、(1)が欲しい復調信号そのものですから、問題になるのは(2)の復調波の二倍高調波、ということになります。 通常、復調波は音声信号帯域ですから、送信側で含まれる信号の帯域は(電波法で)決まっています。ならば、(1)の信号は通すが、(2)の周波数はカットしてしまうような低域フィルタを入れてしまえば問題は解決します。 それでは、解答に移ります。 1…入出力特性は二乗特性ですから、正しい記述です 2…不要な2倍高調波は低域フィルタでカットするので正しい記述です 3…入力が大きくても、直線検波より低歪となることはないので誤りです 4…検波出力のうち、歪となるのは第2高調波なので正しい記述です となりますから、正解(誤った記述)は3と分かります。 | |
 |
 |