回路網キルヒホッフの第一法則キルヒホッフの第二法則起電力の総計電圧降下の総計ループノード - １アマの無線工学 H19年12月期 A-03

□ H19年12月期 A-03 Code:[HB0101] : 複数の電圧源と抵抗からなる回路網の計算（キルヒホッフの法則）

検索サイトから来た方は…
無線工学の基礎トップへ

以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます

■ 無線工学を学ぶ

(1) 無線工学の基礎

年度別出題一覧

H11年 4月期,8月期,12月期

H12年 4月期,8月期,12月期

H13年 4月期,8月期,12月期

H14年 4月期,8月期,12月期

H15年 4月期,8月期,12月期

H16年 4月期,8月期,12月期

H17年 4月期,8月期,12月期

H18年 4月期,8月期,12月期

H19年 4月期,8月期,12月期

H20年 4月期,8月期,12月期

H21年 4月期,8月期,12月期

H22年 4月期,8月期,12月期

H23年 4月期,8月期,12月期

H24年 4月期,8月期,12月期

H25年 4月期,8月期,12月期

H26年 4月期,8月期,12月期

H27年 4月期,8月期,12月期

H28年 4月期,8月期,12月期

H29年 4月期,8月期,12月期

H30年 4月期,8月期,12月期

R01年 4月期,8月期,12月期

R02年 4月期,9月期,12月期

R03年 4月期,9月期,12月期

R04年 4月期,8月期,12月期

分野別出題一覧

A 電気物理, B 電気回路

C 能動素子, D 電子回路

E 送信機, F 受信機

G 電源, H アンテナ&給電線

I 電波伝搬, J 計測

■ サイトポリシー

■ サイトマップ[1ama]

■ リンクと資料

■ メールは下記まで

2022年

12/31 12月期問題頁掲載

09/01 08月期問題頁掲載

05/14 04月期問題頁掲載

H1912A03 Counter

無線工学 > １アマ > H19年12月期 > A-03
A-03	図に示す直流回路において、直流電流Ｉ₁＝2 [A]及びＩ₂＝4 [A]がそれぞれ矢印の方向に流れているとき、抵抗Ｒ₃ [Ω]に流れる電流Ｉ₃及び端子ａｂ間の電圧Ｖ_abの大きさの値の組合せとして、正しいものを下の番号から選べ。

	Ｉ₃	Ｖ_ab
１	6 [A]	2 [V]
２	6 [A]	4 [V]
３	2 [A]	2 [V]
４	2 [A]	3 [V]
５	2 [A]	4 [V]

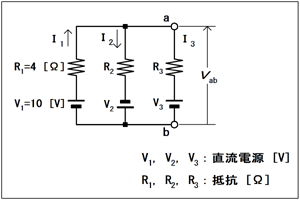
問題図 H1912A03a

Fig.H1912A03a

電圧源が複数あって、簡単な計算では電流値が出てきそうにないので、ここは「キルヒホッフの法則」にお出ましいただくしかなさそうです。［１］キルヒホッフの法則とは何か　キルヒホッフの法則は、第１法則と第２法則の２つからなっていて、「言われてみれば、当然か」の内容で、どっちが第１でどっちが第２だったか、なんてあまり関係ありません。が、ここでは一応区別するために「第１」「第２」と分けて書きます。キルヒホッフの第１法則　回路網の任意の１点に流入する電流の代数和はゼロである…こんな書き方されたら、普通理解できませんよね。でも大学ではこうやって教えてたんです。　要するに、どういうことか…Fig.HB0101_cで言うと、ノードＡに流れ込んでいる電流（Ｉ₁とＩ₂の合計）と流れ出している電流Ｉ₃が等しい、ということです。考えてみれば当たり前な話で、電流は電子の流れなので、電子が勝手に消えて無くなったり、銅線の中から湧いて出てきたりせず、「入ってきたものは必ず出て行く」のですから。キルヒホッフの第２法則　回路網の任意の閉回路において、各部分の電圧降下の代数和はその回路に含まれる起電力の代数和に等しい…とこれもそのままでは何だかよく分かりませんね。　「回路」というからにはひとつ以上のループ部分があるわけですが、そのループの経路に沿って一周する時、抵抗分（交流回路ではインピーダンスでも成り立つ）によって降下する電圧をすべて足し合わせたものと、電源による起電力をすべて足し合わせたものが等しい、と言っているのです。［２］キルヒホッフの法則を使った実際の計算　第１法則は、流れ込む電流の呼び名と向きを決めて方程式を作るだけでよいので、割と式は立てやすいのですが、問題は第２法則です。
ここでは、第２法則をもう少し図で具体的に説明します。再びFig.HB0101_cのループ１の部分に着目して下さい。ループの方向を緑の矢印の方向に取ります。電圧降下の和は、電流がループの方向と同じ時は＋を、逆向きの時は－を取って計算します。すなわち、ループ１について、　電圧降下の総計＝Ｉ₁Ｒ₁＋(－Ｉ₂Ｒ₂) となります。起電力の総計はよく間違えますが、ループの向きに進むと電位が上がるものは＋、下がるものは－で計算します。すなわち、　起電力の総計＝(＋Ｅ₁)＋(－Ｅ₂)	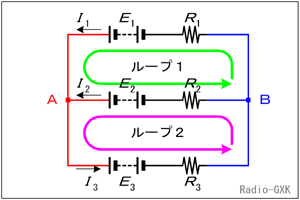Fig.HB0101_c ノードとループの取り方
となります。これももう一段踏み込んで、どういうことなのか考えてみると、　電圧降下の総計＝起電力の総計なので、「電圧降下の総計」を右辺に移項すれば、　起電力の総計－電圧降下の総計＝０となります。（再び）要するに、ループをぐるっと廻って一回戻って来ると、電位差は零、すなわち元の電位に戻る、ということです。　重ねて注意しなければならないのは、ループの向きと電流（電圧降下）の向きや起電力の向きです。これらの取り方によって、符号が反対になりますから、計算が合わなくなります。　なお、問題によっては、あらかじめ電流の向きが与えられていますが、そうでない時は自分で電流の向きを「適当に」決めてやります。もし、方程式を解いた結果、電流の値がマイナスになった場合は、最初に決めた電流の方向と、物理で決まる電流の方向が逆だった、ということになります。　また、［３］「重ねの理」も使える　ここで、少し高級（でも簡単）な解き方を追加します。キルヒホッフだけでも問題は解けますが、電圧源や抵抗の数が少ない場合など、別の方法で解いた方が簡単な場合もあるので、それを紹介します。　この解き方のベースになっている回路定理を、重ねの理、と言います。ここでは定理の証明などは行ないません。　この方法は、理想電源を複数含む回路網の場合についてのもので、実際に計算する場合の手順は、　(1) 電圧源（電流源）を一つ残し、　(2) 残りの電圧源（電流源）は全て短絡（開放）として回路を解き、　(3) これを順に残りの電圧源（電流源）について行い、　(4) 最後に各枝の電流を全て加算するという方法です。これではどう計算していいのか全く分かりませんので、上のFig.HB0101_cで考えてみます。　まずこの回路は電圧源（電池の記号）が2つですから、(1)と(2)の手順を2回繰り返します。まず、Ｅ₁を残して、Ｅ₂をショートしたと考えて、Ｉ₁₁、Ｉ₁₂、Ｉ₁₃（各々Fig.HB0101_c中のＩ₁、Ｉ₂、Ｉ₃に相当）を求めます。　次に、Ｅ₂を残して、Ｅ₁をショートしたと考えて、Ｉ₂₁、Ｉ₂₂、Ｉ₂₃を求めます。　あとは、　Ｉ₁＝Ｉ₁₁＋Ｉ₂₁　…(1) 　Ｉ₂＝Ｉ₁₂＋Ｉ₂₂　…(2) 　Ｉ₃＝Ｉ₁₃＋Ｉ₂₃　…(3) で、各部の電流が求められます。電圧源やノードがこれより多い回路でも、方法は同じです。　一見、手数が多くてキルヒホッフより面倒な気もしますが、一つを残して電圧源をショートしてしまえば、ほとんどの場合は合成抵抗の問題に帰着できますので、電圧と電流の両方の向きと符号の対応を間違えないように、方程式を立てなければならないキルヒホッフよりは楽です。　ただ、この方法でも、電流の向きと符号は間違いのないように注意して下さい。また、ダイオード等の「非線形素子」（電流と電圧が比例しない）が入っていると、重ねの理は成立しません。［４］電源の向きに注意　起電力は電池の記号になっていますが、本当はこれは「電圧源」と考えます。方程式を解いていくと、電池に電流が流れ込むことになるケースがあります（１アマでは出ないようですが）。現実にある電池に（起電力とは逆方向の）電流が流れ込むと「充電」になってしまい、答えが合っているのか悩んでしまいますが、「電圧源」であれば、起電力の向きだけがあって内部抵抗がゼロという「物理モデル」であって、逆方向の電流も流せるからです。それでは、解答に移ります。　分かっているのは、Ｖ₁、Ｒ₁、Ｉ₁、それにＩ₂だけで、後はまったく分からない、こんなので解けるのかと思いますが…実はこの問題、長々とキルヒホッフの法則を説明してきましたが、ほとんどオームの法則だけで解けてしまいます（一応、キルヒホッフの法則は使います）。　まず最初に着目するのは、Ｒ₁とＶ₁のかたまりです。ノードｂ（電源Ｖ₁の負側）を基準に考えると、Ｖ₁だけ上昇した電位から流れ出た電流で、Ｒ₁Ｉ₁の電圧降下が起こるので、ノードａの電位Ｖ_a（＝Ｖ_ab）は、　Ｖ_a＝Ｖ₁－Ｒ₁Ｉ₁＝10－4×2＝2 [V]　…(a) 次に着目するのは、ノードａの電流の収支です。問題には親切に矢印が付いていますので、電流の方向が分かります。キルヒホッフの第１法則をこのノードに適用すれば、流れ込む方向を正として、次のような方程式が立ちます。(Ｉ₃は未知数ですので、正になるか負になるか分かりませんが、正なら流れ込む方向、負なら流れ出す方向、ということになります。）　Ｉ₁－Ｉ₂＋Ｉ₃＝4－2＋Ｉ₃＝０　…(b) 　∴　Ｉ₃＝2 [A]　→2 [A]の流れ込みとなります。従って、\|Ｉ₃\|＝2 [A]、Ｖ_ab＝2 [V]で、正解は３であることが分かります。