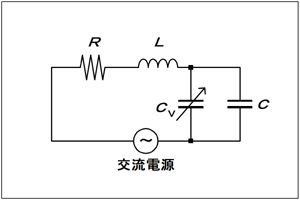
| □ H19年12月期 A-04 Code:[HB0404] : バリコンを含む直列共振回路で共振周波数が与えられた時のCやQの値の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||||||||||||||
| |||||||||||||||||||||||||||
この問題で問われているのは、抵抗がある場合の直列共振回路についてです。その前に、まず「共振とは何か」を考えた後、問題の回路にかかります。[1]共振の本質とは高周波回路、ことに無線に関係する回路の動作や無線機・アンテナの調整にいたるまで、この「共振」という現象を抜きにしては語れません。そこで、「そもそも回路が共振するというのは(物理現象として)どういうことか」ということから始めます。これを理解していれば、フィルタ回路や、送受信機の回路動作など、他のジャンルの問題を解くことが可能になります。(ここでは、直列共振回路の共振のメカニズムまでを記述します。並列回路や、回路のQまで含めた記述は別の問題を参照して下さい。) | |
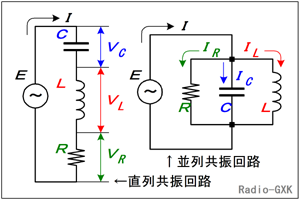 Fig.HB0404_a 直列・並列共振回路 |
まず始めに基本的な事柄の確認ですが、回路の共振には、Fig.HB0404_a左のような直列共振と、その右のような並列共振があります。無線の回路で多く見られるのは並列共振回路の方です。 ここでよくこの両者を見比べてみて欲しいのですが、「直列」の方はLCR三素子に共通なのは流れている電流です。途中で電子が増えたり減ったりはしませんから、これは明らかです。一方、並列の方では三素子にかかる電圧が共通です。これも、3つとも同じ電源に繋がれているので当然といえば当然です。 |
|
以下の図では、交流回路ですから、電流・電圧をベクトルで表記します。この方法に慣れていない方は、是非ともベクトル表記に慣れて下さい。私も高校1年で「交流理論」なる本を借りて読んだ時は、ワケが分からず瞬間睡眠したものですが、今になってこんな便利なものがあるのか、と思います。 余談はさておき、「直列共振回路では、各素子に流れている電流は同じだが、素子の両端に生じている電圧は各々大きさも向き(ここで言う「向き」は電圧ベクトルの向きなので、実は位相のこと)も違う」「並列共振回路では、各素子にかかる電圧は同じだが、素子に流れる電流は各々大きさも向きも違う」ということを頭に入れて下さい。 電源電圧や電流、各素子にかかる電圧や流れる電流をFig.HB0404_aのように取ります。図の中の斜体文字の電圧や電流はベクトル量であることを示します。文章の中では基本的にはすべてベクトル量(複素数)とします。 [2]回路のインピーダンスと共振周波数Fig.HB0404_a左の直列共振回路の合成インピーダンスZsを考えます。直列ですから単純にRCL各素子のリアクタンスをXR=R,XC=−1/(ωC),XL=ωLとして足せばよいので、Zs=XR+j(XC+XL) =R+j(ωL−1/ωC) …(1) となります。共振周波数を求めるには、Zsの大きさが最小になればよく、虚数部分(青字の部分)=0と置いて、共振周波数fRを求めれば、よく知られた fR=1/{2π√(LC)} …(2) が出ます。ところで、さらりと「虚数部分をゼロにすればいい」と書いてしまいましたが、これは非常に深い意味を持ちます。この後も何度か出てきますから、意味を理解して下さい。 「インピーダンスの虚数部分をゼロにする」ということの意味は、電源にそのインピーダンスを負荷として接続した時、電圧の位相と電流の位相がずれないようにできる、ということを意味します。相手が抵抗だけであれば位相はずれませんが、インダクタンス分やキャパシタンス分が含まれると、電圧に対して電流が遅れたり進んだりします。つまり、「共振させる」ということは、インダクタンス分とキャパシタンス分が逆符号で打ち消しあうような回路の状態にする、ということを意味します。 一方、電源電圧Eは、(共振していようがいまいが)全ての素子の両端に生じた電圧の(ベクトル的な)和ですから、 VR=IR VC=−jI/ωC VL=jωIL と置いて、 E=IZs=I{R−j/(ωC)+jωL} =VR+VC+VL …(3) と表せます。共振した時は、(3)式の中にjの項(青字の項)がゼロになってしまう、ということです。 [3]電源周波数と回路の動作下のFig.HB0404_bを見ながら考えて行きましょう。 | |
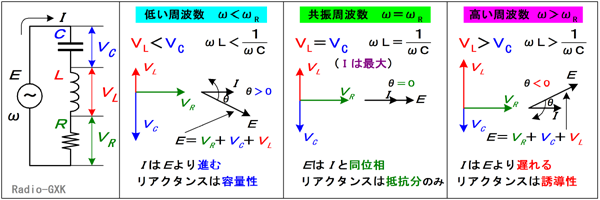 Fig.HB0404_b 直列共振回路と電源周波数 | |
(1) 電源周波数が共振周波数より低い時まず、電源周波数ω(=2πf)が共振周波数ωR(=2πfR)より低い時は、容量性リアクタンスXC(=1/ωC)と誘導性リアクタンスXL(=ωL)を比べると、XC>XLとなっています。要するに、周波数が低いので、コンデンサのリアクタンスよりコイルのリアクタンスの方が小さいのです。ここで、前の方で挙げた、「直列回路では流れる電流が全素子に共通」ということを思い出して下さい。電流Iが共通ですから、リアクタンスの大きい方、すなわちコンデンサの両端の電圧の方がコイルのそれより大きくなります。この状態をベクトル図で描くと、Fig.HB0404_b左のようになります。VLとVCは、向きが互いに逆で、その大きさを比べると、VL<VCです。電源電圧ベクトルEは、(3)式で表されますから、この図で行くと水平線(抵抗両端電圧VRや電流Iの向き)より下に来ます。つまり、電源電圧Eを基準にすると電流Iは(位相が)進んでいるという状態になります。(ちなみに、抵抗の両端の電圧VRと電流Iの位相は同じです。)このような状態を、回路のリアクタンスは容量性であるといいます。式で言うと、(1)式のjの係数が負、ということになり、電源から見ると、キャパシタンス分が多く見える、ということです。 (2) 電源周波数が共振周波数より高い時上とは全く逆の理由で、XC<XLとなります。今度は、周波数が高いので、コイルのリアクタンスよりコンデンサのリアクタンスの方が低いのです。また、コイルの両端の電圧の方がコンデンサのそれより大きくなります。この状態をベクトル図で描くと、Fig.HB0404_b右のようになります。VL>VCです。電源電圧ベクトルEは、水平線より上に来ます。つまり、電源電圧Eを基準にすると電流Iは遅れているという状態になります。このような状態を、回路のリアクタンスは誘導性であるといいます。式で言うと、(1)式のjの係数が正、ということになり、電源から見ると、インダクタンス分が多く見える、ということです。(3) 電源周波数が共振周波数と等しい時この状態が「共振状態」です。容量性リアクタンスと誘導性リアクタンスは、XC=XLの状態で、コンデンサの両端の電圧とコイルのそれが大きさが等しくなります。この状態をベクトル図で描くと、Fig.HB0404_b中のようになります。VLとVCは、向きが互いに逆で、大きさが等しいので、ベクトルの和では零となり、合成後のベクトル中には図の垂直方向の成分は現れてきません。すなわち、回路は誘導性でも容量性でもなくなり、式で言うと、(1)式のjの係数が0、ということになって、電源から見ると、抵抗しか繋がっていないように見える、ということです。 この時、回路で起こっている物理的な現象は何か、というと、コンデンサやコイルはそれぞれ電界(電気力線)や磁場(磁力線)、という形でエネルギーを蓄える装置ですが、これらは互いに振動する逆方向の電圧(電流は共通)に応じてエネルギーをやり取りしています。「電圧が最大の時に最大のエネルギーを蓄えるコンデンサ」と、「電流が最大の時に最大のエネルギーを蓄えるコイル」が、互いに180°ずれた電圧を振動させながらエネルギーをやり取りしているわけです。この振動数は容量とインダクタンスで決まります。共振状態では、この2個の素子の持つ固有の振動数と電源周波数がぴったり合うため、外(電源)から見ると同じ大きさで逆向きの電圧が合成された結果、見えなく(0 [V])なり、抵抗分だけが残るというわけです。 [4]直列共振回路の端子電圧とQ直列共振回路が共振している時は、Fig.HB0404_bの真中のベクトル図や等式不等式が成り立っています。式だけではよく分からないので、箇条書きで要約すれば、(1) コイルとコンデンサの両端の電圧は、大きさが同じで極性が逆 (2) 電源から見ると、抵抗しか繋がっていないように見える (3) 電流Iは電源電圧Eと同位相で、共振していない時に比べ最大値をとる ということです。ならば、コイルとコンデンサの両端の電圧と、抵抗の両端の電圧はどういう関係になっているのでしょうか? 抵抗の両端に生じる電圧の大きさはRI [V]、コイルの両端に生じる電圧の大きさは、IXL=ωLI [V]です。ちなみに、コンデンサの両端に生じる電圧の大きさもIXC=I/ωC [V]でコイルの電圧と同じです。ここで、両者(抵抗とコイル)の比率を取って、 Q=ωLI/RI=ωL/R …(4) という値を定義してしまいましょう。要するに、Qは抵抗の両端の何倍の電圧がコイル(またはコンデンサ)の両端に生じているかという値だというわけです。ちなみに、抵抗両端の電圧VRは電源電圧Eと位相も大きさも同じです。 実際のコイルとコンデンサのみ(抵抗がない)からなる直列共振回路では、Qが数10〜数100程度です。ということは、電源電圧が数[V]でも、コンデンサやコイルの両端には数100 [V]が発生する、ということですので、これだけの耐圧がないと絶縁破壊を起こします。バッテリー駆動のモービル機であっても、高周波出力回路の充電部に触れると危険だ、というのはこのあたりの原理に起因します。 それでは、解答に移ります。 まず、この問題では、損失分(抵抗)が含まれていますが、(2)式からも分かるように、直列共振回路の場合、共振周波数は抵抗には関係ありません。つまり、共振周波数fRはインダクタンス分Lと全容量CPで決まります。つまり、 fR=1/{2π√(LCP)} …(a) となります。また、CPは固定コンデンサ(容量C)と可変コンデンサ(容量Cv)の並列ですから、合成容量CPはこれらの和で、 CP=C+Cv …(b) となります。(a)に(b)を代入してCvについて解けば、 Cv=1/{L(4π2fR2)}−C …(c) となります。(c)式にfR=7050 [kHz]、L=2 [μH]、C=100 [pF]を代入すると、 Cv=255−100=155 [pF] となります。一方、Qは(4)式より、 Q=44.3 となりますから、3が正解と分かります。 | |
 |
 |