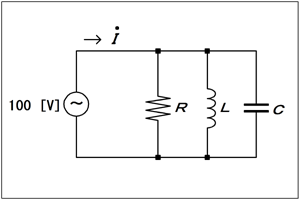
| □ H19年12月期 A-05 Code:[HB0302] : RLCのそれぞれのリアクタンスから並列回路の合成インピーダンスを計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
容量性(コンデンサ)、誘導性(コイル)、抵抗の3つのインピーダンスが直列、並列に組み合わされた回路の合成インピーダンスの問題で、よく出題されます。インピーダンス計算の基本だからでしょう。[1]複素数計算にチャレンジしてみよう2アマまでは実数の世界で何とか解いていましたが、1アマになったら複素数(=実数+虚数 の形の数)計算にチャレンジしてみて下さい。というのも、こういった直列や並列の回路の合成インピーダンスを求める時、複素数でインピーダンスを計算すると、オームの法則だけで解けてしまうからです。2アマの時のようなベクトル計算や直角三角形の1辺の長さを求める公式も(全然無縁なわけではありませんが)使いません。ただ、少しだけ面倒なのは、分数で答えが出た時に分母が複素数になってしまった時、実数部と虚数部を明確に分けるため、「通分」のような「正規化」という作業が必要になることです。でも、慣れてしまえば大して難しくはありません。 この問題では回路の要素(抵抗・コンデンサ・コイル)は3つですが、上に書いたことは、要素がいくつでも使えます。2個や4個になっても、合成抵抗の計算と同じようにやって行けば良いのです。流れる電流も、遅れ位相なのか、進み位相なのか、電流の虚数部を電圧と比較すればすぐに分かります。こんな便利な複素数を使わない手はありません。 [2]複素数を使って解いてみるでは、具体的に見て行きましょう。回路の要素が並列、直列に3つ繋がるパターンはFig.HB0302_aの2種類です。 | |
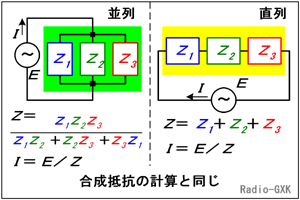 Fig.HB0302_a 3つのインピーダンスの並列・直列 |
これ以外のパターンもありますが、これは別途問題があるので、そこで解いています。 この図で、Z1〜Z3はどれが抵抗・コンデンサ・コイルであるかの組合せは全く任意です。どんな組合せでも合成インピーダンスZは各図の下にある式で表されます。合成抵抗を計算する式と全く同じです。 Z1〜Z3に、抵抗なら抵抗値R [Ω]を、コイルなら誘導性インピーダンスjXLを、コンデンサなら容量性インピーダンス−jXCを代入します。 |
|
ここで、複素数計算のミソは、Fig.HB0302_a並列回路のような、分数になる場合です。途中の計算経過では、分母が複素数になっても構いませんが、最終的に答えにする場合にはこの後に述べるように、分母に共役複素数をかけて実数にします。これを「正規化」といいます。 あとはこれに問題の数値を代入し、複素数の計算をガチャガチャとやるだけです。複素数の計算練習はここではやりませんので、慣れていない方は、同様の問題をいろいろ解いてみて下さい。 [3]並列回路の場合はアドミッタンスで簡単に上の計算で、並列回路では大概の場合、ややこしい分数になって、間違いやすい計算を処理しなければなりません。しかし、アドミッタンスという便利なものを知っていると、簡単に計算できます。そこで、もっとスマートに計算をこなしたい方のために、この方法を試してみます。 | |
|
ここでも同じように3個のインピーダンス要素(Z1, Z2, Z3 [Ω])が並列に電源に接続されているものとします(Fig.HB0302_b)。 今、各々の素子に、インピーダンスの逆数=アドミッタンスY1, Y2, Y3 [S]を定義します。つまり、 Y1=1/Z1 …(1) Y2=1/Z2 …(2) Y3=1/Z3 …(3) です。単位[S]はジーメンスと読みます。 さらに、これらの合成アドミッタンスYを、 Y=Y1+Y2+Y3 …(4) |
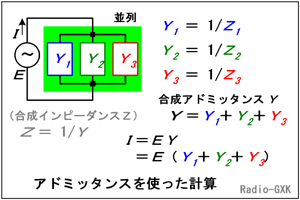 Fig.HB0302_b 並列回路のアドミッタンス計算 |
|
と定義します。直列回路の場合と似てきました。上で計算したような、複雑な分数式もありません。 電源電圧をE [V]、流れる電流(これを求めたい)をI [A]とすると、 I=EY …(5) となります。複素数の計算で面倒な除算がなく、乗算だけで求められるので、並列回路の場合はこの方法が便利です。但し、(1)から(3)のアドミッタンス計算で、どれかのインピーダンスが純虚数や実数でない場合(要するにZ1からZ3のいずれかが複素数)は、この計算だけに複素数の除算が入ります。 それでは、解答に移ります。 (最初にインピーダンスで解き、次にアドミッタンスで解いてみます) この問題はFig.HB0302_aの左のパターンの並列の場合です。問題中の以下の値を代入します。問題文は容量性と誘導性のインピーダンスに虚数単位jと符号が付いていませんのでご注意下さい。 Z1=R=25 [Ω] Z2=XL=j100 [Ω] Z3=XC=-j20 [Ω] と置きます。合成インピーダンスZは、 Z=Z1Z2Z3/(Z1Z2+Z2Z3+Z3Z1) =RXLXC/(RXL+XLXC+XCR) …(a) ={25×j100×(-j20)}/{25×j100+j100×(-j20)+(-j20)×25} =50000/(j2500+2000−j500) =25/(1+j) …(b) 電源から流れる電流Iは、電源電圧をEとして、 I=E/Z=100(1+j)/25=4+j4 [A] と出るので、正解は5と分かります。 次に、アドミッタンスを使って解いてみます。 この問題は、要素のインピーダンスが全て実数(抵抗)又は純虚数(インダクタ、又はキャパシタ)ですので、簡単に求められるパターンです。まず、各々のアドミッタンスを求めます。 Y1=1/Z1=1/25=0.04 [S] Y2=1/Z2=1/XL=1/j100=-0.01j [S] Y3=1/Z3=1/XC=1/(-j20)=0.05j [S] これらの合成アドミッタンスYは、 Y=Y1+Y2+Y3=0.04+0.04j=0.04(1+j) [S となります。電源から流れる電流I [A]は、電源電圧をE [V]として、 I=EY=100×0.04(1+j)=4+j4 [A] と求められ、上の結果と比較すると、全く同じです。しかし、計算はインピーダンスでゴリゴリ解く方法よりも大変スマートです。 余談ですが、この電流は、虚数部の符号が正なので、電圧に対して進んでいることが分かります。また、電流の「絶対値」は、√(42+42)=4√2 [A]と求められます。 | |
 |
 |