| □ H20年08月期 A-04 Code:[HB0107] : ポテンショメータと負荷の電流・電圧からスライダの位置を求める |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||
| |||||||||||||
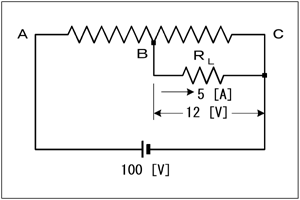
キルヒホッフも必要なく、オームの法則しか出てこないので、簡単なはずなのですが、計算が面倒です。私が解いたら、二次方程式まで出てきてしまいました。どなたか、簡単に計算できる方法をご存知でしたら、教えて下さい。行列式を使って、スマートに解くとか…[1]オームの法則に従って方程式を立てるまず、この回路ですが、ポテンショメータです。普通は、Bがスライドできるようになっている可変抵抗です。 | |
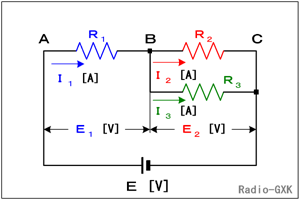 Fig.HB0107_a 各抵抗に着目した電流と電圧 |
さて、今後どんな問題が出題されるか分かりませんので、この問題に特化した数値ではなくて、文字式にして解いて行きます。 Fig.HB0107_aのように、電圧や電流を取ります。まずは、当たり前な方程式から。 E=E1+E2…(1) I1=I2+I3 …(2) また、問題の中で、ポテンショメータの全抵抗(A−C端の抵抗値)R0が与えられている場合は、 R0=R1+R2 …(3) も条件に加わります。 |
|
この他、R1〜R3にかかっている電圧と電流について、オームの法則から、 E1=I1R1 …(4) E2=I2R2 …(5) E2=I3R3 …(6) の合計6本の方程式ができます。後は、問題で与えられている数値を既知数として、未知数について解いてゆく「だけ」ですが、この「だけ」の中身は、ひたすら計算なので、慌てず間違えないようにして下さい。 (ここでは、問題が何を求めているかによって、計算の過程が異なるので、方程式を立てるところまでに留めます。具体的な計算は、解答の中で行ないます。 それでは解答に移ります。 (以下、数式に単位を省略します。)まず、E1は与えられている数値と(1)から簡単に求められて、 E1=E−E2=100−12=88 …(a) です。また、I3=5 [A]なので、(2)式は、 I1=I2+5 I1−I2=5…(b) と変形できます。ポテンショメータの抵抗値については、(3)式から、 R1+R2=10 R1=10−R2…(c) と変形できます。ここで、(4)と(a)及び(5)から、 I1=88/R1 …(d) I2=12/R2 …(e) と変形して、(d),(e)を(b)に代入すると、 88/R1−12/R2=5 …(f) となります。ここでさらに、(f)のR1を(c)で置き換えて、 88/(10−R2)−12/R2=5 …(g) 途中の計算は省略しますが、(g)は R22+10R2−24=0 …(h) となって、R2の二次方程式が出てきます。「何だ、あの(中学で習った)二次方程式の解の公式かよ…忘れちまったな。」と思いますが、良く眺めてみると、(h)式は (R2−2)(R2+12)=0 …(i) と因数分解できる(足して10、掛けて-24になる数は…とやる)ので、R2=2 or -12となります。マイナスの抵抗はありえないので、ここは、 R2=2 [Ω] となりますから、正解は4と分かります。 私も計算が苦手なので、この量の計算になると、必ずと言っていいほど、桁の違う答えしか出てこなかったり、√の中がマイナスになったりしてうんざりしますが、一つ言えることは、変数が山ほどあって、既知数も山ほどある場合は、必要以外の未知数は方程式の中に入れないことです。既知数は既知数で数式の中に織り込んでしまい、最終的に要らない未知数(今回ならR1やI1を消去して、早く求める未知数R2だけの方程式を作ってしまうことです。この道筋が見通せれば何とかなるんですが、普段紙とペンで計算を繰り返していないと、私のようになかなか上達しません。 もし、上手く因数分解できなかったら、正直に二次方程式 ax2+bx+c=0 の解の公式、 x={-b±√(b2−4ac)}/2a を使って下さい。 | |
 |
 |