| □ H20年08月期 A-24 Code:[HB0203] : オシロの波形から周期波形の周期・振幅・平均値・位相差の読取り |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||||||||||||
| |||||||||||||||||||||
| |||||||||||||||||||||
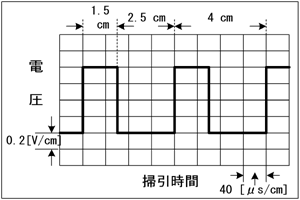
この問題は、デジタル波形です。周期と周波数のみが問われていますが、他のパラメータも勉強しておきましょう。[1]周期と周波数単純な繰り返し波形の場合、その繰り返しの1回の波形の時間長さが周期T [s]です。周期がTのデジタル信号の周波数f [Hz]は、アナログ信号と全く同様に、T=1/f [s] …(1) 又は、 f=1/T [Hz] …(2) の関係があります。国家試験とはあまり関係ありませんが、オシロスコープやロジックアナライザ(ロジアナ)で波形を見ている場合、デジタル信号の場合は高周波や音声と違って、(クロックラインなどを除いて)非周期波形であることが多いので、一見周期波形に見えても注意が必要です。 [2]デューティー比デューティー比はDuty Ratioと書きますが、デジタル信号でこの用語を使う場合は、全体の周期Tのうちの、信号がHである割合をいいます。無線で扱う高周波や音声信号は、正弦波かそれに近いものが多いので、電位の基準に対してほぼ対称な波形ですが、デジタル信号は1周期の中に、どれだけの割合でHとLが存在しうるかは、全くの任意にできます。最近のデジタル回路では、クロックの立上がりエッジと立下がりエッジの両方を使って動作するもの(PCのDDRメモリなど)が増えてきました。このようなケースでは、デューティー比が50 [%]でないと、1周期の中で、処理時間が短くなったり長くなったりして誤動作が起こったりしますから、基準が厳しく決まっています。 [3]位相最後に、交流の性質の中で、最も理解しにくい「位相」について理解しましょう。ご説明はいまさら要しないかもしれませんが、交流、というのは「周期波形」です。同じ形の波が時間とともに何度も繰り返されている、という性質です。1秒間に何度繰り返されるか、が「周波数」であり、波の高さが「振幅」です。どれも波の形が一つ描かれていれば、計測できるものです。 ところが、「位相」というのは、2つの波形の時間差やある基準時間からの差がないと議論できないので、分かりにくいのです。繰り返し波形を一つ持ってきて「この交流の位相は?」という質問は成り立ちません。 | |
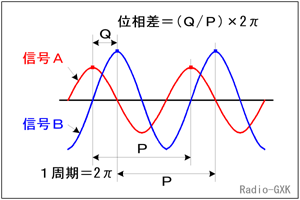 Fig.HB0203_a 交流波形の位相差 |
「位相」は、2つの波形が半周期分ずれたタイミングで存在する時、180度(又はπ [rad])の位相差、1周期分ずれている時は「360度(又は2π [rad])の位相差」といいます。また、一つの波形で議論する時は、波形上の一点を取り、次の周期の同じ点までの位相差を「360度(又は2π [rad])の位相差」と言います。要するに、ある波形と波形の時間差、あるいは同じ波形でも基準からの時間差を周期で割って角度にしたものが「位相差(又は位相)」ということになります。 |
|
Fig.HB0203_aで説明すると、2つの波形の周期がそれぞれP [s]で、山の「頂上」で比較した場合、その時間差がQ [s]だとすると、位相差φ [rad]は、 φ=(Q/P)×2π [rad] (又は(Q/P)×360 [度]) …(3) となります。普通、電気の世界で位相を表す場合は360 [度]が2π [rad]の弧度法を用いますので、この表現に慣れて下さい。 なお、ここでは波形の「山の頂上」で比較しましたが、「谷底」でも上昇又は下降方向のゼロクロス点同志で比較しても、全く同じ議論です。 それでは、解答に移ります。 この問題では、デューティー比と位相は問われていません。周期と周波数のみを考えればいいのです。 まず、周期を求めます。同じ波形の繰り返しですから、立上がりや立下りなど同じ部分を取り出し、その時間差を求めます。問題図中にそれが書かれているので、そのまま利用します。 「繰返し周期」は4 [cm]分の時間です。掃引時間が40 [μs/cm]と書かれていますから、1 [cm]が40 [μs]に相当する、という意味です。ですから、画面上の4 [cm]は、4 [cm]×40 [μs/cm]=160 [μs]となります。ここまでくれば正解したも同然です。周波数は周期の逆数なのですから、1/(160 [μs])=6.25 [kHz]となり、正解は3と分かります。 なお、問題図中に1.5 [cm]や2.5 [cm]という記述があり、この問題を解くのには使いませんが、デューティー比は 1.5/(1.5+2.5)×100=37.5 [%] となります。 | |
 |
 |