| □ H30年04月期 A-24 Code:[HH0204] : 進行波電力と反射波電力、VSWRの測定と計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| ||||||||||||
| ||||||||||||
これまで、進行波電力と反射波電力が分かっていて、VSWRを求める問題ばかり出題されていましたが、今回はちょっとひねってあって、進行波電力とVSWRが分かっている時に、反射波電力を求めるようになっています。計算はひと手間増えますが、同じ公式を使えばいいだけです。[1]そもそも、定在波って何だ?「定在波って何だ?」と行く前に、まず、伝送線路(平たく言えばケーブル・フィーダー)には、送信機からアンテナに向かう「進行波」(問題では「入射波」と記されることもある)と、アンテナから送信機に戻ってくる「反射波」の2種類の波(エネルギーの流れ)が行き交っていることを考えます。 | |
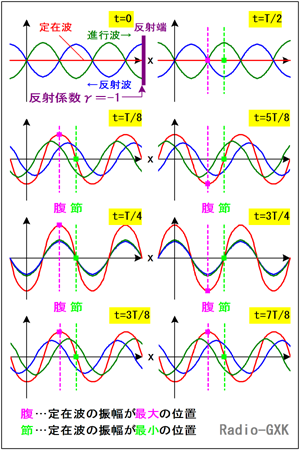 Fig.HH0204_a 進行波・反射波・定在波 |
それを絵にしてみたのがFig.HH0204_aです。この絵は、縦軸が電圧で横軸が波の進行方向の空間的位置を、左上から下の方に、また、右上から下の方に時間経過を書いています。なお、この線路の損失は考えません。本当は動画で見るともっと分かりやすいのですが、技術がないので、こんな静止画で勘弁してください。 右側に波を全反射する反射端があって、緑色の進行波と青い反射波が流れています。ちなみにこの反射端は(後で述べる)反射係数が-1で、実際の回路で言うと「短絡」になります。 図中のTは流れている単一周波数正弦波の周期で、t=0においては、左上のような状態になっているものとします。この状態では、入射波と反射波を合成した赤色の「定在波」(今はこういう名前の波だ、と思って下さい)は、双方の振幅がどの場所でも絶対値が同じで負号が逆なので、まっ平らになります。 図はT/8ごとの様子を書いていますが、赤の「定在波」に着目してみると、t=T/4とt=3T/4の時に振幅が最大に、t=0とt=T/2の時にゼロになります。また、特徴的な振幅の「位置」に着目してみると、常に振幅がゼロの点と大きく振れる点があり、それらの点は移動していません。これらをそれぞれ「節」と「腹」といい、振幅の分布が動かないために「定在波」というわけです。 |
つまり、定在波とは「進行波と反射波が干渉してできる、節や腹が動かない振幅の分布」ということになります。ここで気をつけたいのは、定在波は進行波と反射波の電圧(電流もある)を足した「振幅の分布の形」をいうのであって、進行波や反射波のように、エネルギーを運ぶ波ではありません。同じ「波」という語なので、紛らわしく直感的ではありませんが、それは、この後にもっと一般的な場合について調べる際に、この「波」が正弦波でないことからも分かります。[2]一般的な定在波(反射係数が±1でない)はどうなっているのか?上では、反射係数が-1(短絡の全反射)という特別な例を扱いました。ちなみに、反射係数が+1(開放)の全反射でも、定在波の腹と節の位置が逆になるだけで振る舞いは同じです。普通、負荷が「開放」や「短絡」の状態はVSWRは∞ですから、何らかのアンテナを繋いでこんな状態になることはまずありません。では、反射係数が±1以外の値を取った時はどうなるでしょうか? 反射係数γは一般的に複素数ですが、ここではそんなことは気にせず考えてみます(γが複素数になるのは、反射の際に位相がずれることを考慮に入れるためです)。ここでも無損失な伝送線路を仮定しますが、損失が大きくない限りは以下に述べる定性的な特徴は、我々がアンテナとリグを繋ぐケーブルの中で起こっていることとほとんど変わりありません。 | |
|
Fig.HH0204_bのように、長さがL [m]で特性インピーダンスがZ0 [Ω]の伝送線路(ケーブル)にZL [Ω]の負荷を繋いで、反射係数がγであったとします。 ここで、γの大きさは、「負荷」としてアンテナや抵抗等の受動素子を接続している限りは0≦|γ|≦1になることに注意します。この時の定在波の振幅分布Vsを求めます。 負荷に入射する進行波の振幅をVf [V](線路が無損失なので、実はどこでも振幅は同じ)として、負荷を接続した点を原点に取り、電源に向かう方向(要するに反射波が進む方向)を正に取ると、原点からの位置d [m]における定在波の振幅Vs [V]は次式で表されます。 |
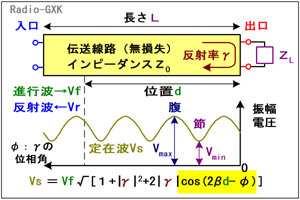 Fig.HH0204_b 任意の反射係数の時 |
|
Vs(d)=Vf√[1+|γ|2+2|γ|cos(2βd−φ)] …(1) となります(試験対策ではこの式は暗記する必要はありません)。 この式で、γは複素数なので、その大きさを求めるために|γ|としていますが、本質的には反射係数の大きさです。βは[1]で挙げたβと同じ(=2π/λ)です。また、cosの項で、φはこのγの位相角を意味しますが、負荷が決まっている限り変わらない量で、ここでは議論の本質ではないので、「そんなものがあるんだ」程度に考えて下さい。 この関数が何を意味するのか考えてみます。まずは関数の形をよく見て下さい。特に、√の中です。定数の1と|γ|はdによって変化しない定数です。また、cosの項は位置によってその値が正弦波的に変化します。従って、この√の中は、直流分に交流分が重畳したようなものになっています。それを√するので、関数の形としては、Fig.HH0204_bの波形のようになります。 (注意して描いたつもりなので)この波形をよく見て下さい。正弦波ではありません。値の小さい方が曲率が小さくなって(すなわち尖って)います。この波形で、極値(最大値と最小値)はどうなっているでしょうか? すなわち、定在波の一番振幅の大きな位置と小さな位置での振幅はどうなっているか、という問いです。 それを考えるために、右辺の√の中にあるcosの項に着目します。Vsが最大になるのは、cos(βd−φ)が最大の1になる時で、その時の値Vmax [V]は、 Vmax=Vf√(1+|γ|2+2|γ|) =Vf(1+|γ|) …(2) となります。逆に、最小値Vmin [V]は、cos(βd−φ)が最小の-1になる時で、 Vmin=Vf√(1+|γ|2−2|γ|) =Vf(1−|γ|) …(3) となります。 整合が完全に取れていて|γ|=0の時は、(2)と(3)からVmax=Vmin=Vfとなりますので、Fig.HH0204_bの波形には最大値も最小値もなく、まっ平らになります。また、[1]で見たような完全反射(|γ|=1)の時は、Vmax=2Vf、Vmin=0となり、Fig.HH0204_aの赤色のような波形になることが、数式からも分かります。 さらに、|γ|=Vr/Vfであることを考えれば、(2)式と(3)式は、 Vmax=Vf(1+|γ|)=Vf+Vr …(4) Vmin=Vf(1−|γ|)=Vf−Vr …(5) となります。これも、Fig.HH0204_aの図から、定在波の振幅が入射波と反射波の和であることから、定性的にも理解できます。 放送局やレーダーなど、大出力を扱う送信所では、ケーブルの耐電圧を整合状態で設計してしまうと、VSWRが上昇した時に耐電圧を超えてしまうことになります。この他にも、電力増幅段の部品の絶縁破壊など、危険を伴うので、VSWRを監視していて、一定以上になったら出力を止めてしまう保護装置が付いています。 [3]電圧定在波比(VSWR)とは何か、どうやって求めるかさていよいよ、SWRの話に移ります。よくアンテナのSWRと言っているのは、正確には「電圧定在波比」であるVSWRのことです。 | |
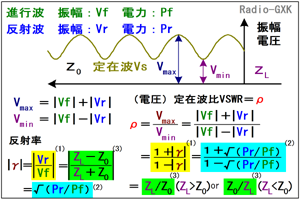 Fig.HH0204_c 電圧定在波比と様々な表現 |
VSWR(値をρとします)は、定在波の最小値Vminに対する最大値Vmaxの比、すなわち、 ρ=Vmax/Vmin …(6) ということです。上で見た((4)式・(5)式)ように、VminとVmaxをそれぞれγで表したものを代入すると、 ρ=(1+|γ|)/(1−|γ|) …(7) とも表せます。[1]で検討したような全反射のケースでは、|γ|=1になるので、分母がゼロとなってρ=∞となるわけです。 |
|
ですが、通常、反射係数というのは直接測定しません。できないわけではありませんが、他の方法があるので、そちらを手段として使います。 その手段の第一は電力の測定です。高周波信号は、普通その実時間波形ではなく電力で強度を表します。実時間波形は高周波になると直接、オシロスコープ等で測定できないからです。VSWRは実際には方向性結合器を内蔵したSWRメーターで測定することが多いです。これが測定しているのは進行波と反射波の電力です。進行波電力Pfと反射波電力Prから反射係数を求めるには、以下のようにします。 |γ|=√(Pr/Pf) …(8) これを(7)式に代入すれば、電力だけでVSWRが、 ρ=[1+√(Pr/Pf)]/[1−√(Pr/Pf)] …(9) と求められます。導出だけでは味気ないので、物理的意味付けをしておくと、インピーダンスが変わらなければ、電圧比は電力比の平方根に比例なので、√の中が電力比になっているわけです。 第二の方法は、伝送線路(ケーブル)のインピーダンスZ0と負荷のインピーダンスZLが分かっている場合、あるいは測定した値から求める方法です。この方法は、電圧定在波だけでなく、電流定在波の検討も必要になるので、式の導出はここでは行ないません(私も教科書を見ないとできません)が、反射係数γは |γ|=|(ZL−Z0)/(ZL+Z0)| …(10) で表されます。これを(7)式に代入すれば、ケーブルと負荷のインピーダンスでVSWRが、 ρ=ZL/Z0 (ZL>Z0の時) or =Z0/ZL (ZL<Z0の時) …(11) となります。但し、この式は、途中で絶対値記号を外しているため、ZLとZ0がともに実数である場合にのみ成り立ちますので、ご注意下さい。ZL>Z0の時とZL<Z0の時で分母分子が逆なので、注意が必要ですが、1アマを受けようという方なら、VSWRが1より小さくなることはないので、もし逆にしていても答えが出た時に気づくでしょう。 まとめると、VSWRは反射係数・進行波と反射波電力・ケーブルと負荷インピーダンスから、以下のように求められます。 ρ=(1+|γ|)/(1−|γ|) …反射係数 (7) ρ=[1+√(Pr/Pf)]/[1−√(Pr/Pf)] …電力 (9) ρ=ZL/Z0 or Z0/ZL …インピーダンス (11) 上記の内容を理解すれば、定性的な記述に正誤をつける問題は解けると思います。また、最近の計算問題では、γの値(複素数)からVSWRを求める問題((7)式の応用)も出ていますが、多くは下の2式(電力とインピーダンス)から求める出題が多いので、これらの式も意味とともに記憶しておく必要があるでしょう。 [4]リターンロスとは何か、どうやって求めるか近年、リターンロス、という用語が選択肢の中などで使用されるケースが出てきましたので、追記します。 | |
|
リターンロス、というのは、信号伝送路にインピーダンスミスマッチがあるとして、入射電力がどの程度反射して戻って来るか(の割合)、を意味します。 Fig.HH0204_dの左側の状態では、伝送線路と全ての接続部分でインピーダンスが整合しているので、入射電力Pfに対して反射電力Prはゼロ(戻り電力なし)です。通常、リターンロスRLは正のデシベル値で表しますので、この図の状態では、 RL(dB)=-10log10(Pr/Pf) =-10log10(0/Pf)=∞ ということになります。 一方、この図の右側のように伝送線路Z0と負荷ZLがミスマッチ(Z0≠ZL)の場合は、 |
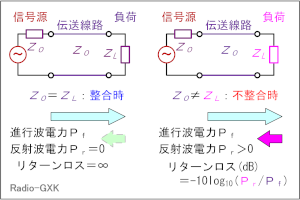 Fig.HH0204_d リターンロスの意味 |
|
RL(dB)=-10log10(Pr/Pf) という値になります。 さらに、もし、ZL=0(短絡)や∞(開放)の場合は、入力電力は全て反射されますから、Pr=PfでPr/Pf=1となり、リターンロスは0 [dB]となります。 リターン(反射波)がどれだけ損失(ロス)になったか、を示す値ですから、反射が多いほど値が小さくなります。 [5]反射係数・VSWR・リターンロス・透過損失ここでは、これまでの伝送線路のまとめとして、反射係数・VSWR・リターンロス・透過損失の数式を挙げておきます。これらの数式は、様々な変形が可能ですが、測定で直接得られやすい、インピーダンス、電力で各値を表すことを考えます。これらのうち、複素数は反射係数だけ、あとは実数(dBも含む)です。まずは、これら4つの値を、線路のインピーダンスZ0、負荷の特性インピーダンスZL(一般的には何れも複素数)で表すことを考えます。 反射係数Γ0は、 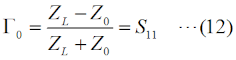 と表せます。S11はSパラメータ(SパラメータについてはH3404A25を参照下さい)です。Z0やZLは一般的には複素数になりますが、伝送線路の損失がゼロもしくは無視できる場合はZ0は実数になります。ZLは、負荷として接続する物に依存します。 VSWRの値ρは、 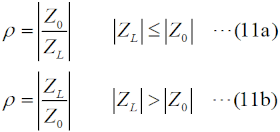 と表せます。|Z0|と|ZL|の大小関係によって、式が異なるので注意して下さい。普段から電波を出していれば、VSWR<1の値が出てきたら、計算がどこかおかしいと気づきますね。 リターンロスRL(dB値)は、 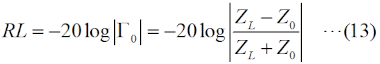 と表せます。この値は、マイナスにはならないので、注意(マイナスになったら、多分logの後の分母分子が逆)して下さい。 最後は、透過損失ですが、これは上で出てきていないので、少し説明が必要です。ただ、考え方は簡単で、Fig.HH0204_dの右で言えば、入力電力のうち負荷に加わった電力の割合(のデシベル値)です。エネルギー保存則から、負荷に透過した電力=入力電力−反射電力、なので、これを分子に、分母は入力電力Pfで表したもので、以下のように表せます。 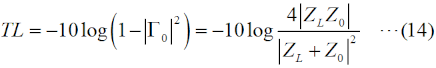 以上が、インピーダンスで表した、反射係数・VSWR・リターンロス・透過損失です。 以下は、入射電力Pfと反射電力Pr(無線の世界では、これが一番測りやすい)で示してみます。但し、電力は位相の情報を持たないので、反射係数は絶対値のみが計算されます。その反射係数(の絶対値)は、 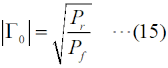 と表せます。VSWRは、 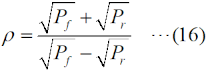 と表せます。リターンロスは、 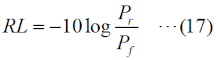 と表せます。透過損失は、 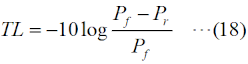 と表せます。 もう一つ、上の式からだけでは変形が面倒なので、リターンロスをVSWRで表した式を示しておきます。 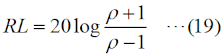 それでは、解答に移ります。 (9)式を使うわけですが、この式をPrについて解く必要があります。あまり複雑な式ではないので、途中は省略しますが、X=√(Pr/Pf)と置いてXについて解いて行き、最後にPrについて解くのが簡単です。 Prについて解いた結果は、以下の式になります。 Pr=Pf{(ρ−1)/(ρ+1)}2 従って、この式にPf=625 [W], ρ=1.5を代入すればよく、 Pr=625×{(1.5−1)/(1.5+1)}2=625×0.22=25 [W] となります。従って、正解は3と分かります。 VSWR=1.5というと、まだまだ調整で落とさなければならない値だ、と思ってしまいますが、電力でいうと、実は送信出力の96%はアンテナから出て行っている、ということになります。 | |
 |
 |