| □ R02年09月期 A-22 Code:[HI0404] : 電波の見通し距離と送受信アンテナ高の計算 |
 検索サイトから来た方は… 無線工学の基礎 トップへ 以下をクリックすると、元のページが行き先に飛び、このウインドウは閉じます |
| ■ 無線工学を学ぶ |
|
(1) 無線工学の基礎 |
|
年度別出題一覧 |
| H11年 4月期,8月期,12月期 |
| H12年 4月期,8月期,12月期 |
| H13年 4月期,8月期,12月期 |
| H14年 4月期,8月期,12月期 |
| H15年 4月期,8月期,12月期 |
| H16年 4月期,8月期,12月期 |
| H17年 4月期,8月期,12月期 |
| H18年 4月期,8月期,12月期 |
| H19年 4月期,8月期,12月期 |
| H20年 4月期,8月期,12月期 |
| H21年 4月期,8月期,12月期 |
| H22年 4月期,8月期,12月期 |
| H23年 4月期,8月期,12月期 |
| H24年 4月期,8月期,12月期 |
| H25年 4月期,8月期,12月期 |
| H26年 4月期,8月期,12月期 |
| H27年 4月期,8月期,12月期 |
| H28年 4月期,8月期,12月期 |
| H29年 4月期,8月期,12月期 |
| H30年 4月期,8月期,12月期 |
| R01年 4月期,8月期,12月期 |
| R02年 4月期,9月期,12月期 |
| R03年 4月期,9月期,12月期 |
| R04年 4月期,8月期,12月期 |
| R05年 4月期,8月期,12月期 |
| R06年 4月期,8月期,12月期 |
|
分野別出題一覧 |
| A 電気物理, B 電気回路 |
| C 能動素子, D 電子回路 |
| E 送信機, F 受信機 |
| G 電源, H アンテナ&給電線 |
| I 電波伝搬, J 計測 |
| ■ サイトポリシー |
| ■ サイトマップ[1ama] |
| ■ リンクと資料 |
■ メールは下記まで |

|
| 2025年 |
| 03/31 R06/12月期問題頁掲載 |
| 03/31 R06/08月期問題頁掲載 |
| 03/31 R06/04月期問題頁掲載 |
| 03/31 R05/12月期問題頁掲載 |
| 03/31 R05/08月期問題頁掲載 |
| 03/31 R05/04月期問題頁掲載 |
|
|
| |||||||||||
| |||||||||||
1アマで見通し距離の計算が出題されたのは、H29年8月期が初めてではないかと思いますが、これまでは、送受信点の両方のアンテナの高さが与えられていて、見通し距離を計算するものでした。今回(R02年9月期)は、一方のアンテナの高さと見通し距離が与えられて、他方のアンテナ高を求める問題です。オームの法則で、電圧と抵抗が既知で電流を求めるか、電流と電圧が既知で抵抗を求めるか、という類ですが、収録してみました。[1]標準大気の意味まず、問題文に「標準大気」とか「等価地球半径」とかいう用語が出てきたら要注意です。地球上の大気は、地表から上空に向かって屈折率が小さくなっています(標準大気)。このような媒質中で、屈折率の分布方向(鉛直方向)からずれた方向に電磁波を伝搬させようとすると、経路が直線で記述できません(要は曲がる、ということ)。このことを考慮に入れて問題を解け、ということです。電磁波の経路を直線で表せるようにするため、地球の半径が大きくなったことにしてしまう、というのが等価地球半径係数Kと呼ばれるものです。K=4/3で、地球の実半径が約6,370 [km]ですから、その4/3で、約8,490 [km]になった、と考えるわけです。この辺りの話は、H1312B05の解説に詳しく書いていますので、ご参照下さい。 [2]見通し距離の計算式ではここから、送受信アンテナ高が与えられている時の、地球上での見通し距離の計算式の導出をやってみます。 | |
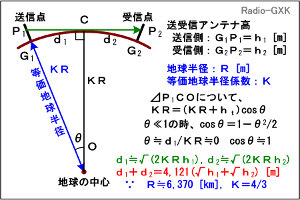 Fig.HI0404_a 標準大気中の到達距離 |
まず、Fig.HI0404_aのように、送受信アンテナ高G1P1、G2P2をそれぞれh1 [m]、h2 [m]とします。等価地球半径KRは8,490 [km]です。こうしてしまえば、電波の経路は直線になりますので、幾何学的に問題を解けばいいことになります。 送信点から電波が地表すれすれを通る、C点までの距離をd1 [m]とし、∠COG1=θ [rad]とします。この図形でd1がいくらになるか、を解いて、受信側も全く同様にd2を求めて両者を足せばいい、という算段で進めます。 △COP1において、各辺の長さについては、 |
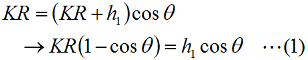 が成立ちます。ここで、直接波の伝搬距離d1はKRに比べて非常に小さいので、 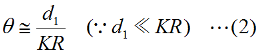 と書けます。また、θも小さいので、三角関数の近似式を使って、(1)式の中のcosθを表現すると、 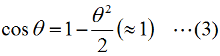 と書けます。これを(1)式のcosθに代入すると、 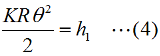 となって、さらにこの(4)式のθに(2)式のθを代入すると、d1が 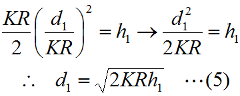 と求められました。あとは、全く同様にしてd2も求めてしまえばよく、 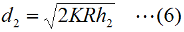 となります。これでd1とd2を足せばよいわけですが、KRは[km]単位で、h1やh2は[m]単位で間違えやすいので、両者を[m]単位に揃えて(送受信点の地上高が[km]単位で書かれることはまずないため)計算すれば、 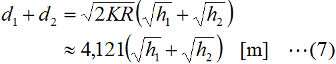 と書けます。あとは、問題に応じてこの式を変形するとか、単位を修正するとかすればよいわけです。 この問題は、地上高x [m]のアンテナから見通せる範囲はどこまでか、という問題(h2=0とすればよい)でもあります。関東では、地上波TVの送信が東京タワー(アンテナ位置を海抜300 [m]とする)から東京スカイツリー(アンテナ位置を海抜600 [m]とする)に変わりました。単純に送信点の高さが2倍になったとして、地上で受信できるカバーエリアは、円の半径にして√2倍(71.4→100.9 [km])、面積にして2倍(16,000 [km2]→32,000 [km2])になったことになります。 実は上記の導出は、1陸技の無線工学Bで出題されたものの、殆どそのままです。 それでは、解答に移ります。 冒頭に書いたように、一方のアンテナ高と見通し距離が与えられていて、他方のアンテナ高を求める問題ですから、(7)式の未知数が変わるだけです。 見通し距離d=d1+d2=20,600 [m]、受信側のアンテナ高h1=1 [m]として(7)式から送信側のアンテナ高h2を求めればよいわけです。 (7)式にd=20600 [m]、h1=1 [m]を代入して、 20,600=4,121×(√1+√h2) …(a) √1+√h2≒5 …(b) ∴ h2≒(5−√1)2=16 [m] となりますから、正解は2と分かります。 | |
 |
 |