ハートレー発振回路部品定数変化発振周波数変化共振回路共振周波数の公式

無線工学 > １アマ > R02年12月期 > A-10
A-10	図に示すトランジスタTrを用いた原理的なコルピッツ発振回路が、1/π [MHz]の周波数で発振しているとき、コイルＬの自己インダクタンス[H]の値として、正しいものを下の番号から選べ。

１	1.00 [mH]
２	1.25 [mH]
３	1.50 [mH]
４	2.00 [mH]
５	2.50 [mH]

Fig.H3212A10a

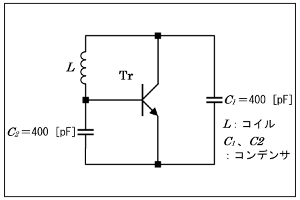
　ハートレーは出題されたことがありますが、コルピッツは今回（2020年12月期）初めてではないかと思います。どちらも、共振回路の共振周波数を求める式が分かれば、容易に解答できると思います。
　下記の解説は、従来の設問に対するものですが、発振周波数を求める計算式が出ていますので、、解答文を参考にして下さい。

［１］共振回路の共振周波数を求める式と部品の定数変動

　ハートレーでもコルピッツでもインダクタンスＬ [H]のコイルと容量Ｃ₀ [F]のコンデンサで組まれた発振回路の発振周波数ｆ₀ [Hz]は、これらのＬとＣで組まれた共振回路の共振周波数そのもので、次のように決まります。
　ｆ₀＝1/2π√ＬＣ₀　…(1)
一方、ここでは、コンデンサの容量が変化してＣ₁になったと言っているので、このときの発振周波数をｆ₁ [Hz]とすると、
　ｆ₁＝1/2π√ＬＣ₁　…(2)
となります。

　問題が要求しているのは、周波数の変化率ｋ [%]ですから、
　ｋ＝(ｆ₁/ｆ₀－1)×100
　　＝{√(Ｃ₀/Ｃ₁)－1}×100…(3)
となります。この値が正なら周波数は上がり、負なら下がることになります。

　ところで、、√の中はＬとＣに対して対称ですから、たとえば、Ｌがｋ [%]変動したとしても周波数の変化率は同じです。

［２］雑談…温度補償用コンデンサ

　セラミックコンデンサのカタログを見ると、「温度補償用」という一群の製品があります。これらは、温度係数が一定の値で、いろいろなものの係数があって選べるようになっています。要するに、温度係数を添加物などで制御して製品としています。
　普通に考えると、温度で変化しない方がいいに決まっているのに、なぜこのような「わざと温度変化する部品」が存在するかと言うと、これは共振回路の「相方」であるコイルの温度変化を打ち消すためです。例えば、温度が20℃変化して、Ｌが0.95Ｌに減少したとすると、Ｃは逆に、1.053Ｃになれば、√の中はほぼ一定ですから、発振周波数に変化はありません。
　しかしながら、これはまだまだ水晶発振子が高価だった頃の話で、ＬＣ発振器でそこまでシビアな設計をするくらいなら、水晶発振子で設計した方が何かと楽だ、という時代になってきました。最近では（温度係数がほぼゼロのものを除き）あまり温度補償用コンデンサに需要がある、という話を聞いたことがありません。

それでは、解答に移ります。
　上記の解説は、「部品の定数に誤差が出た場合の発振周波数の変化」に対するものですが、今回の問題で問われているのは、発振周波数そのものです。上記にあるように、ハートレーでもコルピッツでも、発振周波数を求める式は同じで、ＬＣ共振回路の共振周波数と同じになります。
　ただ、今回の問題のように、コルピッツでコンデンサが２個に分かれている（普通はそうなっていますが）ので、その合成容量が(1)式のＣ₀になります。コンデンサは、「直列」です。その点にだけ、ご留意下さい。
　(1)式をＬについて解いた、
　Ｌ＝(2πｆ₀)^-2/Ｃ₀　…(a)
にｆ₀＝1/π [MHz]、Ｃ＝1/(1/400＋1/400)＝200 [pF]を代入して
　Ｌ＝(2×10⁶)²/(200×10^-12)＝1.25×10^-3 [H]＝1.25 [mH]
となるので、正解は２と分かります。