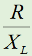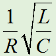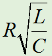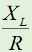共振回路尖鋭度Ｑ共振周波数ピークの1/2の周波数幅Ｑを表す式エネルギー損失

無線工学 > １アマ > R04年04月期 > A-04
A-04	次の記述は、図に示す抵抗Ｒ [Ω]、静電容量Ｃ [F]及びコイルＬ [H]の直列回路について述べたものである。［　］内に入れるべき字句の正しい組合せを下の番号から選べ。ただし、回路は理想的な共振状態にあるものとする。

(1)	回路の点ａｂ間の電圧Ｖ_abは、［Ａ］[V]である。
(2)	Ｌの両端の電圧Ｖ_L [V]の大きさは、ＬのリアクタンスをＸ_L [Ω]とすれば、Ｖの大きさの［Ｂ］倍である。
(3)	回路の尖鋭度Ｑは、［Ｃ］で表される。

	Ａ	Ｂ	Ｃ
１	Ｖ
２	Ｖ
３	0
４	0
５	0

Fig.H3404A04a

　最近、共振現象に関する問題についても、様々な形で出題されるようになりました。共振現象自体を詳しく知りたい方は、H2012A03の解説等を参考にして下さい。ここでは、主に数値的な取り扱いをしますので、数式が続きます。複素数はありますが、微分も積分はありませんし、途中を省略せず、物理的な意味も含めて説明しますので、諦めずに追ってみて下さい。

［１］直列共振回路の復習

　まずは、最初に簡単に直列共振回路の復習をします。

　Fig.HB0405_aに、RLC直列回路と交流電源、それに、この回路のインピーダンス（ベクトル表示）を示します。この例では、コイルのリアクタンスＸ_LがコンデンサのリアクタンスＸ_Cより大きい状態を示しています。
　この回路の、全体のインピーダンス（複素数）は、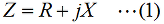
　

で表されます。(1)式の中で、jＸがコイルやコンデンサのリアクタンス分の合計を示しますので、Ｘの値は、

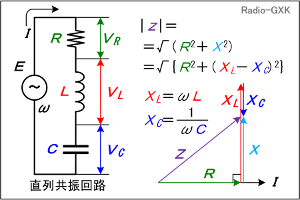Fig.HB0405_a
RLC直列回路のインピーダンス

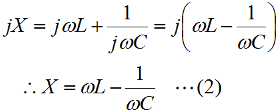となります。直列回路なので、Ｌ、Ｃ各々の要素のリアクタンスを「足した」ハズなのに、虚数の計算のマジックで引き算になっています。ωＬもωＣも0より大きな実数ですから、これらを単純に足しただけなら、どう転んでもゼロにはなり得ませんが、引き算なのでＸがゼロになり得る、というのが、共振回路のミソです。
　さて、この回路全体のインピーダンスＺ（複素数）の大きさ|Ｚ|は、Fig.HB0405_aの右下の直角三角形の斜辺の長さですから、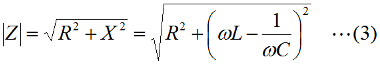
　

と求められます。LCRの直列回路は、共振状態で、この|Ｚ|が最小になる（電流は最大になる）ので、|Ｚ|を最小にする条件を求めてみましょう。その条件とは、(3)式のルートの中のカッコの中身（ωＬ－1/(ωＣ)）が、ゼロになる状態です。すなわち、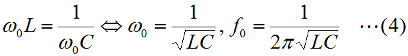
　

となって、おなじみの共振周波数を求める公式が導出できました。
　次に、この時に回路に流れる電流Ｉ₀の大きさを求めておくと、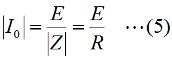
　

となります。共振していない時は、Ｘ≠0ですから、(1)式のjＸも≠0となり、Ｚが複素数になるので、電流も複素数となりますが、共振時の電流は実数です。つまり、電源電圧Ｅの位相と流れる電流Ｉの位相の位相にズレがない状態です。
　さらにインピーダンで説明すると、Fig.HB0405_aのベクトル図で、共振時はＸ_LとＸ_Cの大きさが同じで向きが逆、つまりＺベクトルには上下の成分がなく、「床に寝て」しまい、Ｒと同じ大きさになっている、という状態です。

［２］Ｑの意味するものは何か

　共振のＱというのは、様々な所で出会います。１アマの問題でも、受信機の選択度と絡めて出題されたり、GHzオーダーの回路設計ではなくてはならない、実用面で非常に重要なパラメータです。
　そんなＱの定義式としては、ω₀を共振周波数として、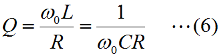
　

という形のものを記憶されている方も多いのではないでしょうか。一方、受信機の選択度や、送信機のスプリアスの抑制などで、「Ｑを大きくすると良い」という記述を目にします。Ｑが大きいほど、共振周波数から少しでもずれると、次段にエネルギーが転送されなくなる（鋭いカットオフ特性を持つフィルタとして機能する）という意味です。
　また、Ｑが大きいほど、回路の損失が少ない、とも言えます。(6)式の定義では、Ｒが分母に来ていて、コイルのリアクタンス（ω₀Ｌ）をＲで割っていますから、式の形からも、Ｑが大きいほど、損失が少ない（一般には）良い回路、ということができます（コンデンサについても同様）。
　Ｑの「本名」をQuality Factorと言いますが、まさに（共振）回路のQualityを定量的に表しているもの、という意味でしょう。
　さらに、Ｑは、(4)式を使ってちょっと変形（ω₀＝1/√(ＬＣ)を(6)式に代入）してやると、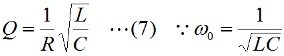
　

という具合に、ＱがＲ,Ｌ,Ｃ各々の値で定まり、共振周波数とは無関係な値として表記することもできます。

［３］Ｑを周波数帯域と結びつけて考える

（以降は「交流回路の基礎理論」（電気学会 2002）p.51を参考にしています）
　さて、上で、Ｑが大きいということは、強い周波数選択性を持つことだ、と書きました。そこで、以降は共振回路の周波数特性とＱとを結びつける作業に入ります。数式が多くなりますが、じっくり追っていって下さい。
　まず、天下り的ではありますが、回路の電流が共振状態から1/√2（直列共振回路の場合）に減少する周波数（共振点を挟んだ両側）を求めます。何故、1/2ではなく1/√2なのか、は後述します。
　電流が1/√2になるのですから、回路のインピーダンス|Ｚ|は共振時の√2倍になればいいわけで、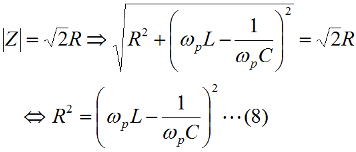
　

という条件が出てきます。ここで、ω_pは、電流値が共振時の1/√2になる時の角周波数です（これが求めるもの）。
　(8)式の両辺の平方根を取れば、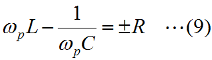
　

となります。さらに、この両辺をω₀Ｌで割る（右辺は(6)式を使う）と、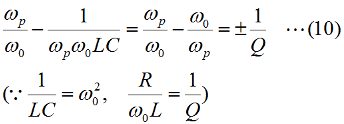
　

となります。何やら面倒くさそうな式になってきましたが、ｘ＝ω_p/ω₀（但し、ｘ＞0）と置くと、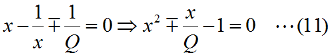
　

となって、ｘの２次方程式となりました。２次方程式が出てきたからには、中学の数学で習った「解の公式」↓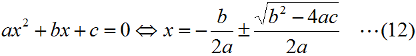
　

にお出ましいただいて、解くしかありません。(11)式には複号が入っていますから、プラスの時とマイナスの時に場合分けして解きます。まずは複号がマイナスの時で、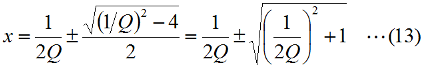
　

と求められますが、√の前の複号のうち、マイナス側はｘ＜0となって条件を満たしませんから、プラス側の解のみを採用します。その時の角周波数をω_p+とすると、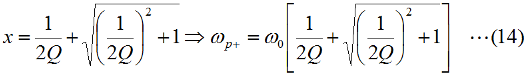
　

と求められます。次に、(11)式の複号がプラスの時の解は、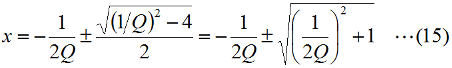
　

となりますが、これも√の前の複号のうち、マイナス側はｘ＜0となって条件を満たしませんから、プラス側の解のみを採用します。その時の角周波数をω_p-とすると、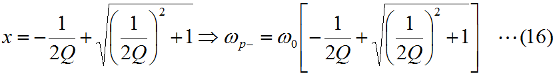
　

と求められます。

　延々と方程式を解いてきましたが、結局、求める共振周波数の上下にある、電流が1/√2になる周波数ω_p+とω_p-は(14)式と(16)式のように求められました。
　さて、ここからは、この周波数の性質です。(14)式と(16)式のω_p+とω_p-の式の形を見て、ピンと来た人は数学のセンスがある人です。まずは、これらを乗算してみます。すると、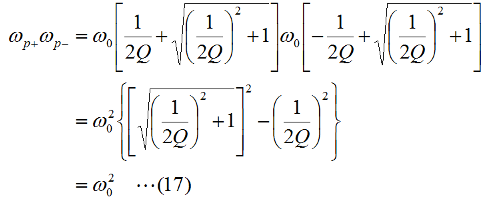
　

と、何ともシンプルな形になりました。(17)式が言っているのは、ω_p+とω_p-の「相乗平均」がω₀になる（√(ω_p+ω_p-)＝ω₀）ということです。別の言い方をすれば、(ω_p+＋ω_p-)/2≠ω₀、つまり、共振周波数ω₀はω_p+とω_p-のセンターに位置するわけではない、ということです。
　蛇足なのでこれ以上計算式は増やしませんが、(14)式と(16)式を足して2で割ってみれば、ω_p+とω_p-の算術平均となる周波数は、(1/2Ｑ)の程度、ω₀より上側にずれていることが分かります。また、そのずれ1/2Ｑは、Ｑが大きいほど小さくなるので、Ｑが十分大きければ、共振周波数はほぼω_p+とω_p-の真中に来る、ということも分かります。
　お次は、周波数幅(ω_p+－ω_p-)とＱの関係です。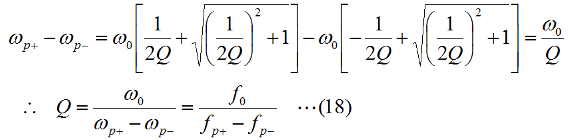
　

となり、共振周波数を周波数幅(ω_p+－ω_p-)で割ったものがＱに等しい、ということが分かります。この（角）周波数幅ω_p+－ω_p-を半値幅と言います。1/√2なのに、なぜ半値幅と呼ぶかと言うと、電流（又は電圧）が元の1/√2ということは、電力に換算した時に、半分の値になるからです。フィルタのカットオフ周波数の表記もアンテナのビーム幅（アンテナの場合は半値角）も、電圧比で通過域や最大放射方向の1/√2となる周波数や角度で表記します。dB表記では、3 [dB]落ち、とよく言います。フィルタで言えば、通過域での通過電力を1 （0 [dB]）とすると、カットオフ周波数での通過電力は1/2（-3 [dB]）ということです。
　この式が意味するのは、Ｑが大きい（損失が少ない）共振回路ほど、ω₀に対する帯域幅ω_p+－ω_p-が狭い、ということです。共振曲線で言えば、Ｑが大きいほど山の形がより尖った形になる、ということです。

【参考文献】
大平孝　「Ｑファクタは七色仮面」電子情報通信学会誌 Vol.99,No.8,2016 pp.856-857
水野皓司　「今更ながら、Ｑって何？」電子情報通信学会誌 Vo.99,No.12,2016 pp.1191-1192

それでは、解答に移ります。

Ａ…	［１］の下の方で述べたように、共振時は(2)式のＸ＝0となり、コイルとコンデンサの直列部分の電圧Ｖ_abは0になります
Ｂ…	Ｖ_L＝ＩＸ_L＝Ｉω₀Ｌ、また、Ｖ_ab＝0なので、Ｖ＝ＲＩ。従って、Ｖ_L/Ｖ＝ω₀Ｌ/Ｒです
Ｃ…	直列共振回路のＱをＲ、Ｌ、Ｃのみで表せば、(7)式になります

となりますから、正解は５と分かります。