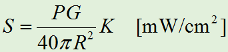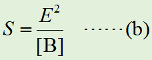自由空間伝搬電力束密度絶対利得空中線電力送受信点間距離伝搬損失等方性アンテナ

次の記述は、電波の強度に対する安全基準を満たす判定のための、電波の強度の算出について述べたものである。［　］内に入れるべき値として、最も近いものの組合せを下の番号から選べ。ただし、無線設備の諸元、平均電力を用いるための換算比及び大地面等の反射を考慮した係数は表のとおりとし、アンテナの水平面内指向特性は全方向性、算出地点はアンテナの主輻射方向であり俯角減衰量は無視できるものとする。また、√(37.7)≒6.14、√(3770)≒61.4及び√π≒1.77とする。

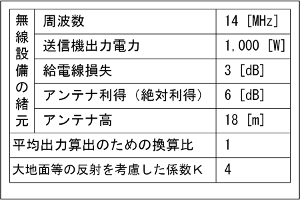Fig.H3404A23a

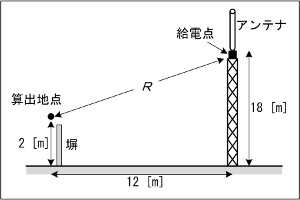Fig.H3404A23b

(1)	図において、算出地点の電波の強度を求めるには、最初にアンテナ入力電力Ｐ [W]、アンテナの主輻射方向の絶対利得Ｇ（真数）、アンテナからの距離Ｒ [m]及び大地面等の反射を考慮した係数Ｋを用いて、次式により電力束密度Ｓ [mW/cm²]の値を算出する。　　表から得られた数値を上式に代入すれば、Ｓ＝［Ａ］[mW/cm²]……(a) となる。
(2)	周波数が30 [MHz]以下の場合、(a)から次式により電界強度Ｅ [V/m]の値を算出する。
(3)	14 [MHz]における電波の強度に対する安全基準は、電界強度又は磁界強度があるが、電界強度の基準値は[MHz]を単位とする周波数をｆとすれば次式から求められる。　電界強度の基準値＝824/ｆ [V/m]……(c) 　(b)から得られた電界強度Ｅと(c)の基準値を比較し、(b)＜(c)であれば、電波の強度に対する安全基準を満たしていることとなる。

	Ａ	Ｂ
１	1/π	37.7
２	1/π	3770
３	1/(2π)	37.7
４	1/(2π)	3770

　一見すると、電波防護指針の問題のようで面食らいますが、中身は「等方的に放射される電波の強さ」を計算する問題です。難しいことを考える必要はありません。

［１］電波の強さの求め方

　法律での規制値は、自由空間に置かれた「理想的な放射源」から、一定距離離れた場所での電力束密度、つまり単位面積あたりに通過する電力をもとにして、その値にある係数を掛けて規定するようになっています。そこで、その「理想的な放射源」や「単位面積あたりの電力」を計算する必要が出てくるわけですが、どのようにしたらよいでしょうか？

［２］理想的な放射源とは

　まず放射源について考えます。電磁波（電波でも光でも）を扱っていると、「等方的な放射源」とか「等方性（アイソトロピック）アンテナ」という言葉が出てきます。この「等方的」というのは、言葉は難しいですが、分かりやすく言えば「どの方向にも同じ強さで放射する（あるいは感度を有する）完全無指向性」ということです。（後で述べますが、現実のアンテナは、最大放射方向が存在し、その方向に絶対利得Ｇという利得を持ちます。）

　このような放射源・アンテナは、現実的に実現可能でない（アンテナの場合、水平面内も垂直面内も無指向性は実現できない）のですが、頭の中で論理を組み立てて「あったとすればどうなるか」を考えてみます。
　まず、原点に電力Ｐ [W]を放射する（等方的な）放射源を置き、原点から距離Ｒ [m]の球面を考えます。この球面上での「単位面積当たりに通過する電波のエネルギーの密度」つまり電力束密度ρ₀ [W/m²]を求めたいのですが、どうすればよいでしょうか？という問題です。
　Fig.HI0801_aのように、球の表面積Ｓは4πＲ² [m²]ですから、

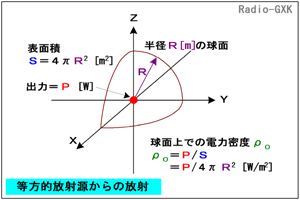Fig.HI0801_a
等方的放射源からの放射

　ρ₀＝Ｐ/Ｓ＝Ｐ/4πＲ² [W/m²]　…(1)
となります。この考え方は、自由空間に置かれた点電荷による電界を求める時に、点電荷を中心に持ってきた球面で包んで、電気力線が球面上で単位面積あたり何本あるか、という方法で算出したのと同じです。
　次に、実際のアンテナでこの電力束密度がどうなるかを考えてみます。上に書いたように、実際のアンテナでは指向性があり、その最大放射方向に絶対利得Ｇ（絶対利得の定義が、等方的放射源の何倍の強さになるか、という指標）なので、それを使ったときの電力束密度ρ [W/m²]は簡単に、ρ₀をＧ倍すればよく、
　ρ＝Ｇρ₀＝ＧＰ/4πＲ² [W/m²]　…(2)
と求められます。

［３］大地の反射を考慮する

　人工衛星局でもなければ、我々が開局する無線局は陸の上（移動局は水の上も空の上もありますが、電力が制限されているので、通常は問題にならない）です。自由空間との大きな違いは、大地という反射面がある、ということです。

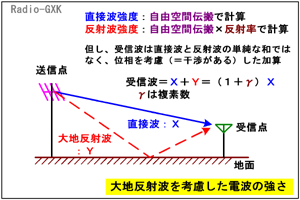Fig.HI0801_b
大地反射波を考慮した電波の強さ

　Fig.HI0801_bのように、受信点（今の場合は人体）では、直接波と大地反射波が合成されて受信されます。この時、注意すべきなのは、受信（照射）される電波の強さは、直接波と反射波の単純な和ではなく、位相を考慮した和である、ということです。
　１アマレベルではないので省略しますが、長さの異なる経路を通ってきた電波が一点で受信されると干渉します。干渉状態での強度は、複素数で計算してやる必要があります。
　ちょっとだけ計算しておきます。直接波の強度をＸ [V/m]、反射波の強度をＹ [V/m]、大地の反射率と経路長差を合わせた係数γと置く（全て位相も考慮した複素数）と、ＹをＸで表せて、

　Ｙ＝γＸ　…(3)
となるので、受信波強度Ｚ [V/m]は、
　Ｚ＝Ｘ＋Ｙ＝（1＋γ）Ｘ　…(4)
となります。法規上の規定が、電界強度ではなく電力で規定されている場合は、(4)式の絶対値の2乗を取って、自由空間のインピーダンスＺ₀（≒120π [Ω]）で割れば、単位面積あたりの電力値に変換できます。
　現実的には、経路差があると言っても、その差はわずかです。つまり、直接波と反射波で、強度はほとんど差はありませんが、位相が異なることによる効果が大です。そこで、受信点（人体）に到達する電力Ｓ [W/m²]が直接波と大地反射波をひっくるめて、直接波のＫ倍になる、と仮定すれば、(2)式から
　Ｓ＝Ｋρ＝ＫＧＰ/4πＲ² [W/m²]　…(5)
と求められます。
　さらに、これを受信点での電界強度（の大きさ）Ｅ [V/m]で表すことを考えると、
　Ｓ＝Ｅ²/Ｚ₀　…(6)
となります。これがなぜこうなるか、はマクスウェル方程式から、平面波のポインティングベクトル（進行方向の単位面積あたりのエネルギーの流れ）というものを求めなければなりませんので、ここでは証明しません。ですが、オームの法則（電力＝電圧²/抵抗）にそっくり（単位面積あたりの電力＝電界強度²/自由空間のインピーダンス）ですから、覚えやすいと思います。
　さて、法律で規定されているＳの単位は、[mW/cm²]です。一方、上で計算してきたのはMKSA単位系で、Ｓの単位は[W/m²]です。両者の変換には、
　1 [W/m²]＝1 [10³mW/10⁴cm²]＝0.1 [mW/cm²]
という係数が必要です。つまり、Ｚ₀≒120π≒377 [Ω]を用いれば、(6)式は、
　Ｓ＝Ｅ²/(377×10)＝Ｅ²/3770 [mW/m²]　…(6)'
と表せる、ということです。

それでは解答に移ります。
　まず、Ａの値を計算する前に、問題の図からＲ [m]を求めます。アンテナ高18 [m]から算出地点の高さ2 [m]を引いて、タワーと算出地点の水平距離12 [m]にピタゴラスの定理を適用すれば、
　Ｒ＝√{(18-2)²＋12²}＝20 [m]
また、その他の値を換算しておきましょう。換算が必要なのは、給電線の損失とアンテナ利得（dB→真数）です。
　給電線損失＝1/2
　アンテナ利得Ｇ＝4
　なお、Ｐはアンテナでの入力で、一方、表の「無線設備の諸元」の値は送信機出力ですから、上記の給電線損失を考慮して、
　Ｐ＝1000/2＝500 [W]
と求めておきます。

Ａ…	上記を問題のＳの計算式に代入して、　Ｓ＝(500×4×4)/(40π×20²)＝1/(2π) と求められます
Ｂ…	(6)'式より、ここに入る数値は3770です

となりますから、正解は４と分かります。